Earlier today Ben Goldacre posted about using Benford’s Law to try and detect fraud in the Russian elections. Read that now, or the rest of this post won’t make sense. This is a loose R translation of Ben’s Stata code.

The data is held in a Google doc. While it is possible to directly retrieve the contents with R, for a single document it is easier to save it a CSV, and load it from your own machine.

russian <- read.csv("Russian observed results - FullData.csv")

There are loads of ways of manipulating data and plotting it in R, and while you can do everything in the base R distribution, I’m going to use a few packages to make it easier.

library(reshape)
library(stringr)
library(ggplot2)

A little transformation is needed. We take only the columns containing the counts and manipulate the data into a “long” format with only one value per row.

russian <- melt(
    russian[, c("Zhirinovsky", "Zyuganov", "Mironov", "Prokhorov", "Putin")], 
    variable_name = "candidate"
)

Now we add columns containing the first and last digits, extracted using regular expressions.

russian <- ddply(
    russian, 
    .(candidate), 
    transform, 
    first.digit = str_extract(value, "[123456789]"),
    last.digit  = str_extract(value, "[[:digit:]]$"))

The table function gives us the counts of each number, and we compare these against the counts predicted by Benford’s Law.

first_digit_counts <- as.vector(table(russian$first.digit))
first_digit_actual_vs_expected <- data.frame(
  digit            = 1:9,
  actual.count     = first_digit_counts,    
  actual.fraction  = first_digit_counts / nrow(russian),
  benford.fraction = log10(1 + 1 / (1:9))
)

The counts of the last digit can be obtained in a similar way.

last_digit_counts <- as.vector(table(russian$last.digit))
last_digit_actual_vs_expected <- data.frame(
    digit     = 0:9,
    count     = last_digit_counts,    
    fraction  = last_digit_counts / nrow(russian)
)
last_digit_actual_vs_expected$cumulative.fraction <- cumsum(last_digit_actual_vs_expected$fraction)

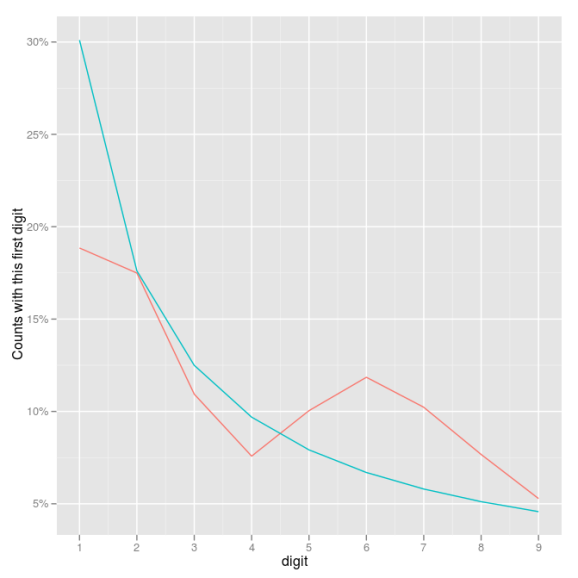
Here is the line graph…

a_vs_e <- melt(first_digit_actual_vs_expected[, c("digit", "actual.fraction", "benford.fraction")], id.var = "digit")
(fig1_lines <- ggplot(a_vs_e, aes(digit, value, colour = variable)) +
    geom_line() +
    scale_x_continuous(breaks = 1:9) +
    scale_y_continuous(formatter = "percent") +
    ylab("Counts with this first digit") +
    opts(legend.position = "none")
)

and the histogram

(fig2_hist <- ggplot(russian, aes(value)) +
    geom_histogram(binwidth = 20)
)