How to Calculate a Partial Correlation Coefficient in R: An Example with Oxidizing Ammonia to Make Nitric Acid
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
Introduction
Today, I will talk about the math behind calculating partial correlation and illustrate the computation in R with an example involving the oxidation of ammonia to make nitric acid using a built-in data set in R called stackloss. In a separate post, I will also share an R function that I wrote to estimate partial correlation. In a later post, I will discuss the interpretation of the partial correlation coefficient at length.
I read Pages 234-237 in Section 6.6 of “Discovering Statistics Using R” by Andy Field, Jeremy Miles, and Zoe Field to learn about partial correlation. They used a data set called “Exam Anxiety.dat” available from their companion web site (look under “6 Correlation”) to illustrate this concept; they calculated the partial correlation coefficient between exam anxiety and revision time while controlling for exam score. As I discuss further below, the plot between the 2 above residuals helps to illustrate the calculation of partial correlation coefficients. The plot above makes intuitive sense; if you take more time to study for an exam, you tend to have less exam anxiety, so there is a negative correlation between revision time and exam anxiety.
They used a function called pcor() in a package called “ggm”; however, I suspect that this package is no longer working properly, because it depends on a deprecated package called “RBGL” (i.e. “RBGL” is no longer available in CRAN). See this discussion thread for further information. Thus, I wrote my own R function to illustrate partial correlation.
Partial correlation is the correlation between 2 random variables while holding other variables constant. To calculate the partial correlation between X and Y while holding Z constant (or controlling for the effect of Z, or averaging out Z),
1) perform a normal linear least-squares regression with X as the target and Z as the predictor
2) calculate the residuals in Step #1
3) perform a normal linear least-squares regression with Y as the target and Z as the predictor
4) calculate the residuals in Step #3
5) calculate the correlation coefficient between the residuals from Steps #2 and #4; the result is the partial correlation between X and Y while controlling for the effect of Z
, of course, is an estimator of the correlation coefficient; 3 such common estimators are the Pearson product-moment correlation coefficient (Pearson’s r), the Spearman rank correlation coefficient (Spearman’s rho), and the Kendall rank correlation coefficient (Kendall’s tau).
Example – Oxidation of Ammonia to Nitric Acid in the Stackloss Data Set
There is a built-in data set in R called stackloss with measurements on operations in a plant that oxidized ammonia (NH3) to make nitridc acid (HNO3). This paper by Taylor, Chilton and Handforth describes the process pretty clearly on its first page.
1) Pass a mixture of air and ammonia through red-hot catalytic wire gauze to make nitric oxide.
4NH3 + 5O2 → 4NO + 6H2O
2) As the nitric oxide cools, it reacts with excess oxygen to make nitrogen dioxide.
2NO + O2 → 2NO2
3) The nitrogen dioxide reacts with water to form nitric acid.
3NO2 + H2O ⇌ 2HNO3 + NO
I want to calculate the partial correlation coefficient between air flow speed and water temperature while controlling for acid concentration. Following the procedure above, here is the plot of the relevant residuals.
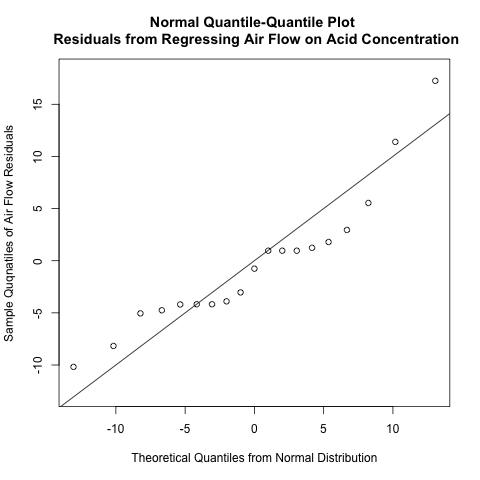
The Pearson correlation coefficient is a commonly used estimator for the correlation coefficient, but hypothesis testing based on Pearson’s r is known to be problematic when dealing with non-normal data or outliers (Bishara and Hittner, 2012). Let’s check for the normality underlying our data. Here is the Q-Q plot of the residuals of regressing air flow on acid concentration.
Note the 2 “dips” below the identity line in the intervals [-5, 0] and [0,10] along the horizontal axis. These “dips” suggest to me that there is a systematic deviation away from normality for these residuals.
Furthermore, recall from my earlier blog post that you can check for normality by the ratio of the interquartile range to the standard deviation. If this ratio is not 1.35, then there is reason to suspect that the distribution is not normal. For the residuals from regressing air flow on acid concentration, this ratio is 0.75, which is far enough away from 1.35 to suggest non-normality.
Given that there are only 21 residuals, and given that the 2 ways to check for normality above suggest non-normality, it is best to conclude that there is insufficient evidence to suggest that the data come from a normal distribution. (This is different from asserting that the data definitely come from a non-normal distribution. Given the low sample size, I just can’t be certain that the population is normally distributed.) Thus, I will not use Pearson’s r to estimate the partial correlation. (Someone with the handle ars in a discussion thread in Cross Validated referred a paper by Kowalski (1972) about Pearson’s r for further thoughts.)
I estimate the partial correlation using Spearman’s rho, which, using the cor() function, is calculated as 0.5976564. However, is this estimate statistically significant? To answer this question, we can conduct a hypothesis test.
For Spearman’s rho, the sampling distribution is
,
where
In our example, T = 3.162624, and the p-value is 0.005387061. Thus, there is evidence to suggest that this correlation is significant.
In comparing Spearman’s rho and Kendalls’ tau in a set of presentation slides titled Overview of Non-Parametric Statistics, Mark Seiss from the Department of Statistics at Virginia Tech stated ”…most researchers conclude there is little basis to choose one over the other”. Thus, I chose to use Spearman’s rho purely out of my familiarity with it. I welcome your comments about why Kendall’s tau is better.
In a discussion at Cross Validated, someone with the handle onestop referred to a paper by Newson (2002) that cited a book by Kendall & Gibbons (1990); onestop reproduced this quotation: ”…confidence intervals for Spearman’s rS are less reliable and less interpretable than confidence intervals for Kendall’s τ-parameters, but the sample Spearman’s rS is much more easily calculated without a computer”. I’m curious about whether or not this result is transferrable to hypothesis testing.
References
Bishara, A. J., & Hittner, J. B. (2012). Testing the significance of a correlation with nonnormal data: Comparison of Pearson, Spearman, transformation, and resampling approaches.
Andy Field, Jeremy Miles, and Zoe Field. (2012). Discovering statistics using R. Sage Publications Limited.
Kowalski, Charles J. “On the effects of non-normality on the distribution of the sample product-moment correlation coefficient.” Applied Statistics (1972): 1-12.
Newson R. Parameters behind “nonparametric” statistics: Kendall’s tau,Somers’ D and median differences. Stata Journal 2002; 2(1):45-64.
Taylor, Guy B., Thomas H. Chilton, and Stanley L. Handforth. “Manufacture of Nitric Acid by the Oxidation of Ammonia1.” Industrial & Engineering Chemistry23.8 (1931): 860-865.
R Script for Entire Analysis
Here is the R code for computing everything in this analysis:
##### Partial Correlation - An Example with the Oxidation of Ammonia to Make Nitric Acid
##### By Eric Cai - The Chemical Statistician
# extract variables from the Stackloss data set (already built in R)
air.flow = stackloss[,1]
water.temperature = stackloss[,2]
acid = stackloss[,3]
# conduct normal linear least-squares regression with air.flow as target and acid as predictor
regress.air.acid = lm(air.flow~acid)
# extract residuals from this regression
residuals.air.acid = residuals(regress.air.acid)
# conduct normal linear least-squares regression with water.temperature as target and acid as predictor
regress.water.acid = lm(water.temperature~acid)
# extract residuals from this regression
residuals.water.acid = residuals(regress.water.acid)
# plot the 2 sets of residuals against each other to see if there is a linear trend
png('INSERT YOUR DIRECTORY PATH HERE/residuals plot air flow and water temperature controlling acid concentration.png')
plot(residuals.air.acid, residuals.water.acid, xlab = 'Residuals from Regressing Air Flow on Acid Concentration', ylab = 'Residuals from Regressing Water Temperature on Acid Concentration', main = 'Partial Correlation Between Air Flow and Water Temperature\n Controlling for Acid Concentration')
dev.off()
# normal q-q plot of residuals of regressing air flow on acid to check for normality
png('INSERT YOUR DIRECTORY PATH HERE/q-q plot air flow residuals on acid concentration.png')
qqplot(qnorm(seq(0,1,length=101), mean(residuals.air.acid), sd(residuals.air.acid)), residuals.air.acid, xlab = 'Theoretical Quantiles from Normal Distribution', ylab = 'Sample Quqnatiles of Air Flow Residuals', main = 'Normal Quantile-Quantile Plot \n Residuals from Regressing Air Flow on Acid Concentration')
# add the identity line
abline(0,1)
dev.off()
# check if the ratio of interquartile range to standard deviation is 1.35 (this is a check for normality)
five.num.summary.airflow.acid = summary(residuals.air.acid)
q3.airflow.acid = five.num.summary.airflow.acid[5]
q1.airflow.acid = five.num.summary.airflow.acid[2]
(q3.airflow.acid - q1.airflow.acid)/sd(residuals.air.acid)
# sample size
n = length(air.flow)
# use Spearman correlation coefficient to calculate the partial correlation
partial.correlation = cor(residuals.air.acid, residuals.water.acid, method = 'spearman')
# calculate the test statistic and p-value of the Spearman correlation coefficient
test.statistic = partial.correlation*sqrt((n-3)/(1-partial.correlation^2))
test.statistic
p.value = 2*pt(abs(test.statistic), n-3, lower.tail = F)
p.value
Filed under: Applied Statistics, Basic Chemistry, Descriptive Statistics, Plots, R programming Tagged: ammonia, applied statistics, basic chemistry, chemistry, correlation, correlation coefficient, descriptive statistics, kendall correlation, kendall correlation coefficient, kendall’s tau, least-squares, linear regression, nitric acid, nitric oxide, nitrogen dioxide, normality, normality test, oxidation, oxygen, partial correlation, partial correlation coefficient, pearson correlation, pearson correlation coefficient, pearson’s r, q-q plot, qq plot, quantile-quantile plot, regression, residual, residuals, spearman correlation, spearman correlation coefficient, spearman’s rho, statistics, water
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.