CanSum problem is a problem where a given array of integers (nums) and a target integer (target), return boolean (TRUE \ FALSE) indicating, that the target integer can be calculated using two or more numbers in array nums.

You may assume that each integer from the array can be used multiple times. You can also assume, that any integer (in nums or in target) is from 0 to +1e9 and the length of the nums array is from 2 to 1000 elements.

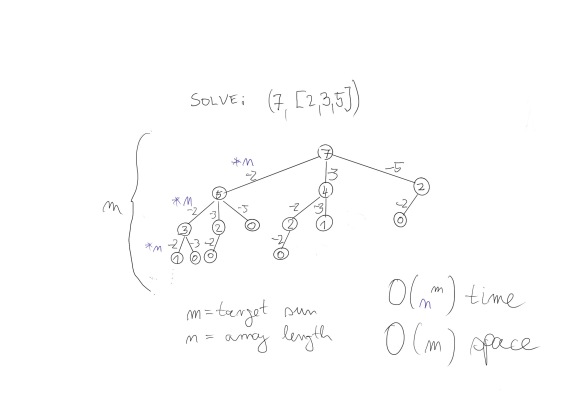
An example to show this problem would be: Find a target 7 with a given array of (2,3,5).

Once we start drawing this tree we will see that some tree nodes are repeating and are recalculated again (e.g.: from 2 to 0 (with -2)). With the use of Big O-notation, we can see, that the solution for this tree is of m-height and of n-length (from root to leave). Each tree node stops when a 0 is reached, which is a solution for each tree.

Brute force with O(n^m) solution

Typical solution is to do a brute force. Calculate all the possible paths in the decision tree. Based on the solution explanation, we can see that the time component is exponential (n^m). Because the tree will calculate the m-depth of the solution for the length of the array. And the bigger the target number or the longer the array is, the longer it will take to calculate the solution.

canSumBF <- function(target, numbers){
  if (target == 0) { return (TRUE) }
  if (target < 0){ return (FALSE) }
  
  for (i in 1:length(numbers)){
    remainder <- target - numbers[i] 
    if (canSumBF(remainder, numbers) == TRUE) {
      return (TRUE)
    }
  }
  return(FALSE)
}

Now, try a simple solution to support the time component of this solution:

canSumBF(7, c(2,3,5))     ## true
canSumBF(87, c(13,10))  ## false
canSumBF(250, c(7,14))  ## false 

Memoization with O(n) solution

With the repetition of subtrees when finding a solution, we can store intermediate subtrees to list of all possible solutions and shorten the amount of time for calculation.

canSumMEMO <- function(target, numbers, memo = list()){
  if (target == 0) { return (TRUE) }
  if (target < 0)  { return (FALSE) }
  if (target %in% names(memo)) {
    return (memo[[as.character(target)]])
  }
  
  for (i in 1:length(numbers)){
    remainder <- target - numbers[i]
    if (canSumMEMO(remainder, numbers[i], memo) == TRUE) {
      memo[[as.character(target)]] <- TRUE
      return (TRUE)
    }
  }
  memo[[as.character(target)]] <- FALSE;
  return(FALSE) 
}

Now, check the solutions with storing intermediate solutions

# test memo
canSumMEMO(250, c(7,14)) ## false 
canSumMEMO(150, c(7,14)) ## false 
canSumMEMO(7, c(2,3,5)) ## true

To make the comparison simpler, let’s encapsulate both functions in Sys.time() function. You can do this with a microbenchmark or any other way.

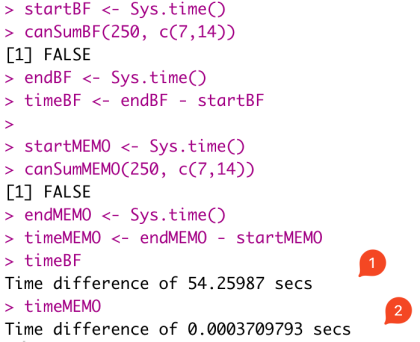
########## compare both solutions

startBF <- Sys.time()
canSumBF(250, c(7,14)) 
endBF <- Sys.time()
timeBF <- endBF - startBF

startMEMO <- Sys.time()
canSumMEMO(250, c(7,14)) 
endMEMO <- Sys.time()
timeMEMO <- endMEMO - startMEMO

And the difference is obvious; 54 seconds for the brute force (timeBF) solution and near 0 seconds for the memoization solution (timeMEMO).

As always, code is available on Github in  Useless_R_function repository. The sample file in this repository is here (filename: TwoSum_CanSum.R) Check the repository for future updates.

Many of the problems can be found on LeetCode website.

Happy R-coding and stay healthy!