What is MANOVA (Multivariate Analysis of Variance)?

• MANOVA is an extension to univariate ANOVA that includes at least two dependent variables to analyze differences between multiple groups in the independent variable.
• In contrast to ANOVA, where we compare individual group means, MANOVA compares the vectors containing the group mean of each dependent variable.
• MANOVA uses omnibus Wilk’s Lambda, Pillai’s Trace (most robust to departures from assumptions), Roy’s Largest Root, or Hotelling-Lawley’s test, which are later converted to F statistics for assessing the significance of the group differences. Pillai’s Trace has the highest statistical power.
• MANOVA maximizes the discrimination in between-groups than within-groups based on best linear combinations of the multiple response variables.

Why MANOVA is useful?

• MANOVA analyzes the differences among groups in an independent variable by considering multiple dependent variables. This reduces the type I error which can be inflated by performing separate univariate ANOVA for each dependent variable.
• MANOVA also controls for inter-correlations among the multiple dependent variables in the dataset.
• As compared to univariate ANOVA, MANOVA uses more information from the dependent variables i.e., MANOVA may find differences between groups based on combined information from the multiple dependent variables.

If there is only one dependent variable is of interest for quantifying the differences between groups, then MANOVA is not necessary.

Assumptions of MANOVA

MANOVA follows similar assumptions as in ANOVA for the independence of observations and homogeneity of variances

In addition, MANOVA needs to meet the following assumption,

• Multivariate normality: data or residuals should have a multivariate normal distribution for each combination of independent and dependent variables (checked by Shapiro-Wilk test for univariate normality and Mardia’s skewness and kurtosis for multivariate normality)
• Homogeneity of the variance-covariance matrices: data should have equal variance-covariance matrices for each combination formed by each group in the independent variable. This is a multivariate version of the Homogeneity of variances that is checked in univariate ANOVA. It can be tested using Box’s M test. Box’s M-test has little power and uses a lower alpha level such as 0.001 to assess the p value for significance.
• Multicollinearity: There should be no multicollinearity (very high correlations i.e., > 0.9) among dependent variables
• Linearity: dependent variables should be linearly related for each group of the independent variable. If there are more than two dependent variables, the pair of dependent variables should be linearly related
• There should be no outliers in the dependent variables (multivariate outliers) (checked by Mahalanobis distances)
• dependent variables should be continuous

MANOVA Hypotheses

• Null hypothesis: group mean vectors are same for all groups
• Alternative hypothesis: group mean vectors are not same for all groups

One-way (one factor) MANOVA in R

In one-way MANOVA, there is one independent variable with two or more groups and at least two dependent variables

Example dataset

Suppose we have a dataset of various plant varieties (plant_var) and their associated phenotypic measurements for plant heights (height) and canopy volume (canopy_vol). We want to see if plant heights and canopy volume are associated with different plant varieties using MANOVA.

For MANOVA, the dataset should contain more observations per group in independent variables than a number of the dependent variables. It is particularly important for testing the Homogeneity of the variance-covariance matrices using Box’s M-test.

Load dataset,

library(tidyverse)
df=read_csv("https://reneshbedre.github.io/assets/posts/ancova/manova_data.csv")
head(df, 2)
# output
  plant_var height canopy_vol
  <chr>      <dbl>      <dbl>
1 A             20        0.7
2 A             22        0.8

Summary statistics and visualization of dataset

Get summary statistics based on each dependent variable,

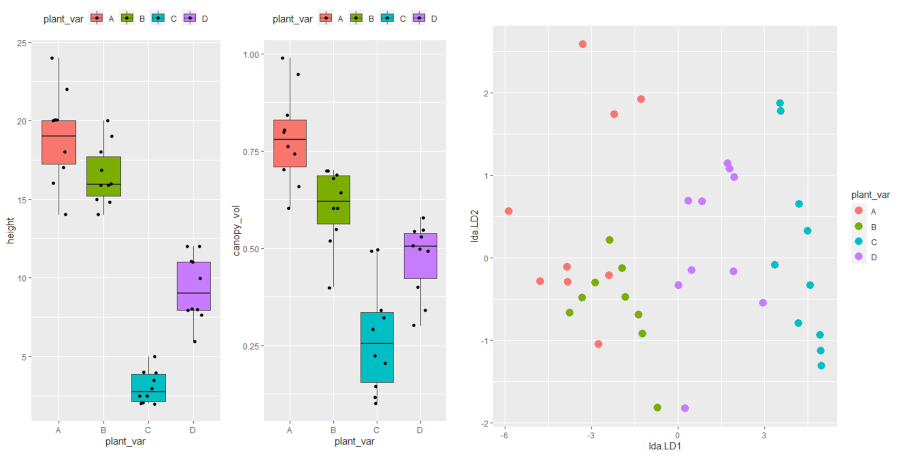
# summary statistics for dependent variable height 
df %>% group_by(plant_var) %>%  summarise(n = n(), mean = mean(height), sd = sd(height))
# output
 plant_var     n  mean    sd
  <chr>     <int> <dbl> <dbl>
1 A            10 18.9   2.92
2 B            10 16.5   1.92
3 C            10  3.05  1.04
4 D            10  9.35  2.11

# summary statistics for dependent variable canopy_vol 
df %>% group_by(plant_var) %>%  summarise(n = n(), mean = mean(canopy_vol), sd = sd(canopy_vol))
# output
  plant_var     n  mean     sd
  <chr>     <int> <dbl>  <dbl>
1 A            10 0.784 0.121 
2 B            10 0.608 0.0968
3 C            10 0.272 0.143 
4 D            10 0.474 0.0945

Visualize dataset,

library(gridExtra)
p1 <- ggplot(df, aes(x = plant_var, y = height, fill = plant_var)) + geom_boxplot(outlier.shape = NA) + geom_jitter(width = 0.2) + theme(legend.position="top")
p2 <- ggplot(df, aes(x = plant_var, y = canopy_vol, fill = plant_var)) + geom_boxplot(outlier.shape = NA) + geom_jitter(width = 0.2) + theme(legend.position="top")
grid.arrange(p1, p2, ncol=2)

Perform one-way MANOVA

dep_vars <- cbind(df$height, df$canopy_vol)
fit <- manova(dep_vars ~ plant_var, data = df)
summary(fit)
# output
          Df Pillai approx F num Df den Df    Pr(>F)    
plant_var  3 1.0365   12.909      6     72 7.575e-10 ***
Residuals 36                                            

# get effect size
library(effectsize)
effectsize::eta_squared(fit)
# output
Parameter | Eta2 (partial) |       95% CI
-----------------------------------------
plant_var |           0.52 | [0.36, 1.00]

The Pillai’s Trace test statistics is statistically significant [Pillai’s Trace = 1.03, F(6, 72) = 12.90, p < 0.001] and indicates that plant varieties have a statistically significant association with both combined plant height and canopy volume.

The measure of effect size (Partial Eta Squared; η_p²) is 0.52 and suggests that there is a large effect of plant varieties on both plant height and canopy volume.

post-hoc test

The MANOVA results suggest that there are statistically significant (p < 0.001) differences between plant varieties, but it does not tell which groups are different from each other. To know which groups are significantly different, the post-hoc test needs to carry out.

To test the between-group differences, the univariate ANOVA can be done on each dependent variable, but this will be not appropriate and lose information that can be obtained from multiple variables together.

Here we will perform the linear discriminant analysis (LDA) to see the differences between each group. LDA will discriminate the groups using information from both the dependent variables.

library(MASS)
post_hoc <- lda(df$plant_var ~ dep_vars, CV=F)
post_hoc
# output
Call:
lda(df$plant_var ~ dep_vars, CV = F)

Prior probabilities of groups:
   A    B    C    D 
0.25 0.25 0.25 0.25 

Group means:
  dep_vars1 dep_vars2
A     18.90     0.784
B     16.54     0.608
C      3.05     0.272
D      9.35     0.474

Coefficients of linear discriminants:
                 LD1        LD2
dep_vars1 -0.4388374 -0.2751091
dep_vars2 -1.3949158  9.3256280

Proportion of trace:
   LD1    LD2 
0.9855 0.0145 

# plot 
plot_lda <- data.frame(df[, "plant_var"], lda = predict(post_hoc)$x)
ggplot(plot_lda) + geom_point(aes(x = lda.LD1, y = lda.LD2, colour = plant_var), size = 4)

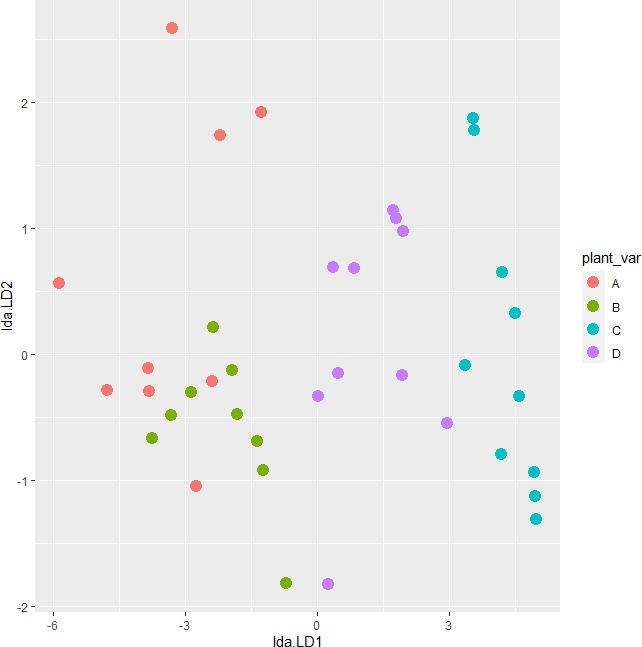
The LDA scatter plot discriminates against multiple plant varieties based on the two dependent variables. The C and D plant variety has a significant difference (well separated) as compared to A and B. A and B plant varieties are more similar to each other. Overall, LDA discriminated between multiple plant varieties.

Test MANOVA assumptions

Assumptions of multivariate normality

This test may not be easy to test as it may not be available in all statistical software packages. You can initially check the univariate normality for each combination of the independent and dependent variables. If this test does not pass (significant p-value), it may be possible that multivariate normality is violated.

Note: As per Multivariate Central Limit Theorem, if the sample size is large (say n > 20) for each combination of the independent and dependent variable, we can assume the assumptions of multivariate normality.

library(rstatix)
df %>% group_by(plant_var) %>%  shapiro_test(height, canopy_vol)
 plant_var variable   statistic     p
  <chr>     <chr>          <dbl> <dbl>
1 A         canopy_vol     0.968 0.876
2 A         height         0.980 0.964
3 B         canopy_vol     0.882 0.137
4 B         height         0.939 0.540
5 C         canopy_vol     0.917 0.333
6 C         height         0.895 0.194
7 D         canopy_vol     0.873 0.109
8 D         height         0.902 0.231

As the p-value is non-significant (p > 0.05) for each combination of independent and dependent variables, we fail to reject the null hypothesis and conclude that data follows univariate normality.

If the sample size is large (say n > 50), the visual approaches such as QQ-plot and histogram will be better for assessing the normality assumption.

Now, let’s check for multivariate normality using Mardia’s Skewness and Kurtosis test,

library(mvnormalTest)
mardia(df[, c("height", "canopy_vol")])$mv.test
# output
          Test Statistic p-value Result
1     Skewness    2.8598  0.5815    YES
2     Kurtosis   -0.9326   0.351    YES
3 MV Normality      <NA>    <NA>    YES

As the p-value is non-significant (p > 0.05) for Mardia’s Skewness and Kurtosis test, we fail to reject the null hypothesis and conclude that data follows multivariate normality.

Here both Skewness and Kurtosis p value should be > 0.05 for concluding the multivariate normality.

Homogeneity of the variance-covariance matrices

We will use Box’s M test to assess the homogeneity of the variance-covariance matrices. Null hypothesis: variance-covariance matrices are equal for each combination formed by each group in the independent variable

library(heplots)
boxM(Y = df[, c("height", "canopy_vol")], group = df$plant_var)
# output
	Box M-test for Homogeneity of Covariance Matrices

data:  df[, c("height", "canopy_vol")]
Chi-Sq (approx.) = 21.048, df = 9, p-value = 0.01244

As the p-value is non-significant (p > 0.001) for Box’s M test, we fail to reject the null hypothesis and conclude that variance-covariance matrices are equal for each combination of the dependent variable formed by each group in the independent variable.

If this assumption fails, it would be good to check the homogeneity of variance assumption using Bartlett’s or Levene’s test to identify which variable fails in equal variance.

Multivariate outliers

MANOVA is highly sensitive to outliers and may produce type I or II errors. Multivariate outliers can be detected using the Mahalanobis Distance test. The larger the Mahalanobis Distance, the more likely it is an outlier.

library(rstatix)
# get distance
mahalanobis_distance(data = df[, c("height", "canopy_vol")])$is.outlier
# output
 [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[18] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[35] FALSE FALSE FALSE FALSE FALSE FALSE

From the results, there is no multivariate outliers (all is.outlier = FALSE or p > 0.001) in the dataset. If is.outlier = TRUE, it means there is a multivariate outlier in the dataset.

Linearity assumption

Linearity assumption can be checked by visualizing the pairwise scatterplot for the dependent variable for each group. The data points should lie on the straight line to meet the linearity assumption. The violation of the linearity assumption reduces the statistical power.

library(gridExtra)
p1 <- df  %>% group_by(plant_var) %>% filter(plant_var == "A") %>% ggplot(aes(x = height, y = canopy_vol)) + geom_point() + ggtitle("Variety: A")
p2 <- df  %>% group_by(plant_var) %>% filter(plant_var == "B") %>% ggplot(aes(x = height, y = canopy_vol)) + geom_point() + ggtitle("Variety: B") 
p3 <- df  %>% group_by(plant_var) %>% filter(plant_var == "C") %>% ggplot(aes(x = height, y = canopy_vol)) + geom_point() + ggtitle("Variety: C") 
p4 <- df  %>% group_by(plant_var) %>% filter(plant_var == "D") %>% ggplot(aes(x = height, y = canopy_vol)) + geom_point() + ggtitle("Variety: D") 
grid.arrange(p1, p2, p3, p4, ncol=2)

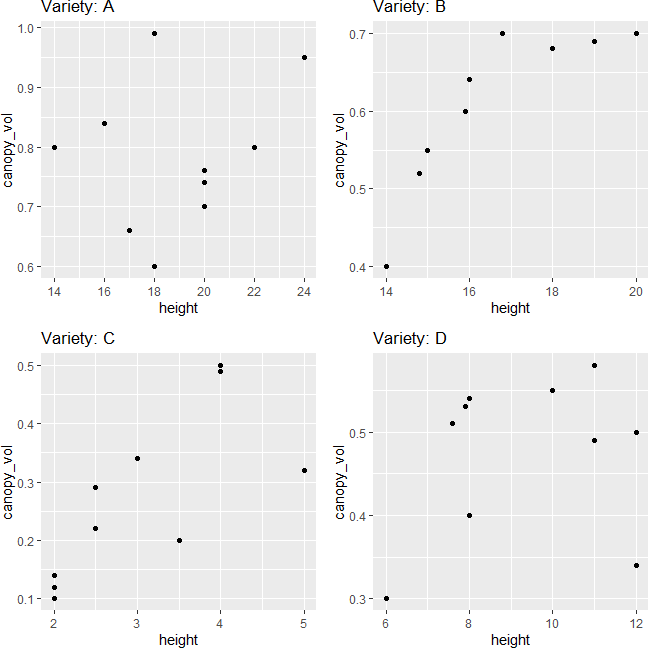
The scatterplot indicates that dependent variables have a linear relationship for each group in the independent variable

Multicollinearity assumption

Multicollinearity can be checked by the correlation between the dependent variable. If you have more than two dependent variables you can use a correlation matrix or variance inflation factor to assess the multicollinearity.

The correlation between the dependent variable should not be> 0.9 or too low. If the correlation is too low, you can perform separate univariate ANOVA for each dependent variable.

cor.test(x = df$height, y = df$canopy_vol, method = "pearson")$estimate
# output
      cor 
0.8652548 

As the correlation coefficient between the dependent variable is < 0.9, there is no multicollinearity.

Learn Data science

Import data into R
Principal component analysis (PCA) code
canonical correlation analysis (CCA) code
Independent component analysis (ICA) code
Cluster Analysis using R
One-way ANOVA using R
Two-way ANOVA using R
Paired sample t-test using R
One sample T-test using R
Random forest in R
Chi-square test in R
Pearson correlation test in R
One Sample t-test in R
ANCOVA using R
Test of Significance

The post MANOVA(Multivariate Analysis of Variance) using R appeared first on Statistical Aid: A School of Statistics.