Veterinary Epidemiologic Research: Count and Rate Data – Poisson & Negative Binomial Regressions
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
Still going through the book Veterinary Epidemiologic Research and today it’s chapter 18, modelling count and rate data. I’ll have a look at Poisson and negative binomial regressions in R.
We use count regression when the outcome we are measuring is a count of number of times an event occurs in an individual or group of individuals. We will use a dataset holding information on outbreaks of tuberculosis in dairy and beef cattle, cervids and bison in Canada between 1985 and 1994.
temp <- tempfile()
download.file(
"http://ic.upei.ca/ver/sites/ic.upei.ca.ver/files/ver2_data_R.zip",
temp)
load(unz(temp, "ver2_data_R/tb_real.rdata"))
unlink(temp)
library(Hmisc)
tb_real<- upData(tb_real, labels = c(farm_id = 'Farm identification',
type = 'Type of animal',
sex = 'Sex', age = 'Age category',
reactors = 'Number of pos/reactors in the group',
par = 'Animal days at risk in the group'),
levels = list(type = list('Dairy' = 1, 'Beef' = 2,
'Cervid' = 3, 'Other' = 4),
sex = list('Female' = 0, 'Male' = 1),
age = list('0-12 mo' = 0, '12-24 mo' = 1, '>24 mo' = 2)))
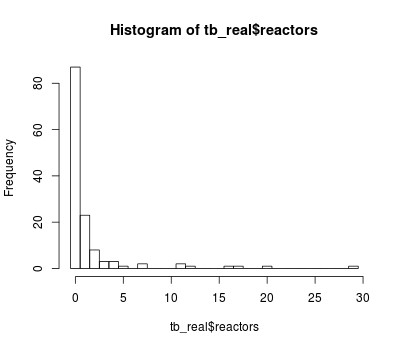
An histogram of the count of TB reactors is shown hereafter:
hist(tb_real$reactors, breaks = 0:30 - 0.5)
In a Poisson regression, the mean and variance are equal.
A Poisson regression model with type of animal, sex and age as predictors, and the time at risk is:
mod1 <- glm(reactors ~ type + sex + age + offset(log(par)), family = poisson, data = tb_real)
(mod1.sum <- summary(mod1))
Call:
glm(formula = reactors ~ type + sex + age + offset(log(par)),
family = poisson, data = tb_real)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.5386 -0.8607 -0.3364 -0.0429 8.7903
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -11.6899 0.7398 -15.802 < 2e-16 ***
typeBeef 0.4422 0.2364 1.871 0.061410 .
typeCervid 1.0662 0.2334 4.569 4.91e-06 ***
typeOther 0.4384 0.6149 0.713 0.475898
sexMale -0.3619 0.1954 -1.852 0.064020 .
age12-24 mo 2.6734 0.7217 3.704 0.000212 ***
age>24 mo 2.6012 0.7136 3.645 0.000267 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 409.03 on 133 degrees of freedom
Residual deviance: 348.35 on 127 degrees of freedom
AIC: 491.32
Number of Fisher Scoring iterations: 8
### here's an other way of writing the offset in the formula:
mod1b <- glm(reactors ~ type + sex + age, offset = log(par), family = poisson, data = tb_real)
Quickly checking the overdispersion, the residual deviance should be equal to the residual degrees of freedom if the Poisson errors assumption is met. We have 348.4 on 127 degrees of freedom. The overdispersion present is due to the clustering of animals within herd, which was not taken into account.
The incidence rate and confidence interval can be obtained with:
cbind(exp(coef(mod1)), exp(confint(mod1)))
Waiting for profiling to be done...
2.5 % 97.5 %
(Intercept) 8.378225e-06 1.337987e-06 2.827146e-05
typeBeef 1.556151e+00 9.923864e-01 2.517873e+00
typeCervid 2.904441e+00 1.866320e+00 4.677376e+00
typeOther 1.550202e+00 3.670397e-01 4.459753e+00
sexMale 6.963636e-01 4.687998e-01 1.010750e+00
age12-24 mo 1.448939e+01 4.494706e+00 8.867766e+01
age>24 mo 1.347980e+01 4.284489e+00 8.171187e+01
As said in the post for logistic regression, the profile likelihood-based CI is preferable due to the Hauck-Donner effect (overestimation of the SE) (see also abstract by H. Stryhn at ISVEE X).
The deviance and Pearson goodness-of-fit test statistics can be done with:
# deviance gof pchisq(deviance(mod1), df.residual(mod1), lower = FALSE) [1] 1.630092e-22 #Pearson statistic mod1.pearson <- residuals(mod1, type = "pearson") 1-pchisq(sum(mod1.pearson^2), mod1$df.residual) [1] 0
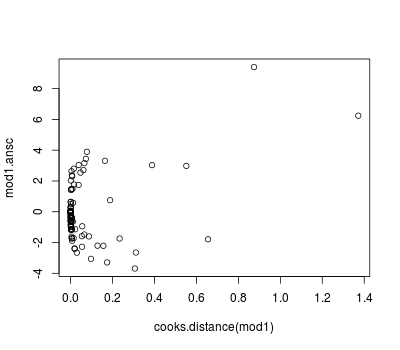
Diagnostics can be obtained as usual (see previous posts) but we can also use the Anscombe residuals:
library(wle) mod1.ansc <- residualsAnscombe(tb_real$reactors, mod1$fitted.values, family = poisson()) plot(predict(mod1, type = "response"), mod1.ansc) plot(cooks.distance(mod1), mod1.ansc)
Negative binomial regression models are for count data for which the variance is not constrained to equal the mean. We can refit the above model as a negative binomial model using full maximum likelihood estimation:
library(MASS)
mod2 <- glm.nb(reactors ~ type + sex + age + offset(log(par)), data = tb_real)
(mod2.sum <- summary(mod2))
Call:
glm.nb(formula = reactors ~ type + sex + age + offset(log(par)),
data = tb_real, init.theta = 0.5745887328, link = log)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.77667 -0.74441 -0.45509 -0.09632 2.70012
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -11.18145 0.92302 -12.114 < 2e-16 ***
typeBeef 0.60461 0.62282 0.971 0.331665
typeCervid 0.66572 0.63176 1.054 0.291993
typeOther 0.80003 0.96988 0.825 0.409442
sexMale -0.05748 0.38337 -0.150 0.880819
age12-24 mo 2.25304 0.77915 2.892 0.003832 **
age>24 mo 2.48095 0.75283 3.296 0.000982 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for Negative Binomial(0.5746) family taken to be 1)
Null deviance: 111.33 on 133 degrees of freedom
Residual deviance: 99.36 on 127 degrees of freedom
AIC: 331.47
Number of Fisher Scoring iterations: 1
Theta: 0.575
Std. Err.: 0.143
2 x log-likelihood: -315.472
### to use a specific value for the link parameter (2 for example):
mod2b <- glm(reactors ~ type + sex + age + offset(log(par)),
family = negative.binomial(2), data = tb_real)
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.