more e’s [and R’s]
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
 Alex Thiéry suggested debiasing the biased estimate of e by Rhee and Glynn truncated series method, so I tried the method to see how much of an improvement (if any!) this would bring. I first attempted to naïvely implement the raw formula of Rhee and Glynn
Alex Thiéry suggested debiasing the biased estimate of e by Rhee and Glynn truncated series method, so I tried the method to see how much of an improvement (if any!) this would bring. I first attempted to naïvely implement the raw formula of Rhee and Glynn
with a (large) Poisson distribution on the stopping rule N, but this took ages. I then realised that the index n did not have to be absolute, i.e. to start at n=1 and proceed snailwise one integer at a time: the formula remains equally valid after a change of time, i.e. n=can start at an arbitrary value and proceeds by steps of arbitrary size, which obviously speeds things up!
n=1e6
step=1e2
lamb=1e2
rheest=function(use=runif(n)){
rest=NULL
pond=rpois(n,lamb)+1
imax=min(which((1:n)>n-pond))
i=1
while (i<=imax){
m=pond[i]
teles=past=0
for (j in 1:m){
space=mean(j*diff(sort(use[i:(i+step*j)]))>.01)
if (space>0){ space=1/space}
else{ space=3}
teles=teles+(space-past)/(1-ppois(j-1,lamb))
past=space
}
rest=c(rest,teles)
i=i+step*m+1}
return(rest)}
For instance, the running time of the above code with n=10⁶ uniforms in use is
> system.time(mean(rheest(runif(n))))
utilisateur système écoulé
6.035 0.000 6.031
If I leave aside the issue of calibrating the above in terms of the Poisson parameter λ and of the step size [more below!], how does this compare with Forsythe’s method? Very (very) well if following last week pedestrian implementation:
> system.time(mean(forsythe(runif(n))))
utilisateur système écoulé
146.115 0.000 146.044
But then I quickly (not!) realised that proceeding sequentially through the sequence of uniform simulations was not necessary to produce independent realisations of Forsythe’s estimate: this R code takes batches of uniforms that are far enough to see a sign change in the differences and takes the length of the first decreasing sequence for each batch. While this certainly is suboptimal in exploiting the n Uniform variates, it avoids scrawling through the sequence one value at a time and is clearly way faster:
fastythe=function(use=runif(n)){
band=max(diff((1:(n-1))[diff(use)>0]))+1
bends=apply(apply((apply(matrix(use[1:((n%/%band)*band)],
nrow=band),2,diff)<0),2,cumprod),2,sum)}
> system.time(mean(fastythe()))
utilisateur système écoulé
0.904 0.000 0.903
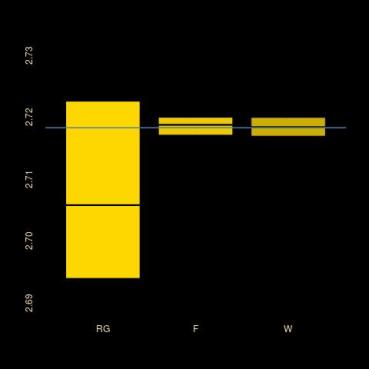
while producing much more accurate estimates than the debiased version if not the original one, as shown by the boxplot at the top (where RG stands for Rhee and Glynn, F for Forsythe and W for Wuber who proposed the original [biased] Monte Carlo estimate of e⁻¹)! Just to make things clear if necessary, all comparisons are run with the same batch of 10⁶ uniform simulations for each mean value entering the boxplots.
One thing that bothers me about the debiased solution is that it is highly sensitive to calibration. For instance, when switching λ and the step size between 10 and 100, I got the following variation over 100 replicates:
 where the last box corresponds to the RG box on the first graph. This is most annoying in that using the whole sequence of uniforms at once and the resulting (biased) estimator leads to the most precise and fastest estimator of the whole series (W label in the first graph)!
where the last box corresponds to the RG box on the first graph. This is most annoying in that using the whole sequence of uniforms at once and the resulting (biased) estimator leads to the most precise and fastest estimator of the whole series (W label in the first graph)!
> system.time(1/mean((n-1)*diff(sort(use))>1))
utilisateur système écoulé
0.165 0.000 0.163
Filed under: Kids, pictures, R, Statistics Tagged: cross validated, debiasing, George Forsythe, Monte Carlo Statistical Methods, R, Russian roulette, simulation, unbiased estimation
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
