Le Monde puzzle [#959]
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
Another of those arithmetic Le Monde mathematical puzzle:
Find an integer A such that A is the sum of the squares of its four smallest dividers (including1) and an integer B such that B is the sum of the third poser of its four smallest factors. Are there such integers for higher powers?
This begs for a brute force resolution checking the integers until a solution appears. The only exciting part is providing the four smallest factors but a search on Stack overflow led to an existing R function:
FUN <- function(x) {
x <- as.integer(x)
div <- seq_len(abs(x))
return(div[x %% div == 0L])
}
(which uses the 0L representation I was unaware of) and hence my R code:
quest1<-function(n=2){
I=4
stop=TRUE
while ((stop)&(I<1e6)){
I=I+1
dive=FUN(I)
if (length(dive)>3)
stop=(I!=sum(sort(dive)[1:4]^n))
}
return(I)
}
But this code only seems to work for n=2 as produces A=130: it does not return any solution for the next value of n… As shown by the picture below, which solely exhibits a solution for n=2,5, A=17864 (in the second case), there is no solution less than 10⁶ for n=3,4,6,..9. So, unless I missed a point in the question, the solutions for n>2 are larger if they at all exist.
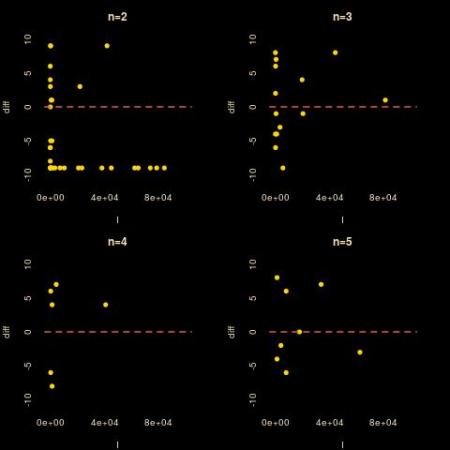 A resolution got published yesterday night in Le Monde and (i) there is indeed no solution for n=3 (!), (ii) there are solutions for n=4 (1,419,874) and n=5 (1,015,690), which are larger than the 10⁶ bound I used in the R code, (iii) there is supposedly no solution for n=5!, when the R code found that 17,864=1⁵+2⁵+4⁵+7⁵… It is far from the first time the solution is wrong or incomplete!
A resolution got published yesterday night in Le Monde and (i) there is indeed no solution for n=3 (!), (ii) there are solutions for n=4 (1,419,874) and n=5 (1,015,690), which are larger than the 10⁶ bound I used in the R code, (iii) there is supposedly no solution for n=5!, when the R code found that 17,864=1⁵+2⁵+4⁵+7⁵… It is far from the first time the solution is wrong or incomplete!
Filed under: Kids, R Tagged: Le Monde, mathematical puzzle, R, Stack Echange
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
