Last Day for Stanton Predictions
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
This week I’ve been looking at two models in R that are attempting to predict whether Giancarlo Stanton would break Roger Maris’ mark of 61 home runs in a season. I’ve not been counting Barry Bond’s official record of 73 home runs because his was a result of the PED’s juicing scandal. However, in my two posts up to now, I made a simple but serious error.
So, before detailing what the error was and how I made it, contrite apologies to Bob Carpenter of the Stan Group. I had misinterpreted a number in his Poisson estimation of the number of at bats Stanton would have left in the season. I’m very sorry Bob for any implied criticism of your model. It really works fine.
My Error
Let me show you first Carpenter’s original model from his blog post and where I goofed. The model:
sum(rbinom(1e5, rpois(1e5, 10 * 555 / 149), rbeta(1e5, 1 + 56, 1 + 555 - 56)) >= (61 - 56)) / 1e5 [1] 0.33376
Note that all the numbers are hard-wired into the model. Sorry, Bob, but this is a bad practice. I have emphasized to students over the last forty years of teaching statistics and quantitative analysis importance of naming variables.
- Give things names and assign values to the names.
That way, you know what you are calculating and can much more easily examine other alternatives. With 10 games left in the season, his estimate makes a lot of sense. I would have liked to match it with Albert’s model with 10 games remaining, but obtaining the data for hitters as of that date is a bit daunting for the purposes of this exercise.
However, with 10 games remaining, Carpenter’s estimate of the at bats remaining for Stanton in the season is 37.2, which amounts to 3.7 per game, a reasonable average. It’s worth noting that Stanton is playing every day to maximize his chances of breaking the record and not getting days off, so 3.7 might be a bit low since his season-long average of 3.72 assumes he probably got a day off every ten games, a value I would have to check after the season.
The Final Predictions
Both models agree that as of Sunday morning, with 1 game to go, Stanton has probably left it too late to catch Maris although he has some chance of catching up to the Babe.
Here is the Albert model with this morning’s data:
set.seed(42) # to get consistent results from run to run
source("pred-hr.R")
model <- pred_hr(hits, "Stanton", standings, 10000)
current_hrs <- model$current_HR
homers <- tibble(hrs = model$future_HR)
ggplot(homers, aes(x = hrs)) + geom_histogram(bins = 20)
print(paste("Probability of tying or breaking the record:",
mean(round(homers$hrs >= (61 - current_hrs), 3))))
print(paste("Probability of tying or breaking 60 (Ruth's mark):", mean(round(homers$hrs >= (60 - current_hrs), 3))))
print(paste("Average number of home runs Stanton will hit =",
round(mean(homers$hrs), 3)))
print(paste("Standard deviation:", round(sd(homers$hrs), 3)))
[1] "Probability of tying or breaking the record: 0.0478"
[1] "Probability of tying or breaking 60 (Ruth's mark): 0.3156"
[1] "Average number of home runs Stanton will hit = 0.367"
[1] "Standard deviation: 0.585"
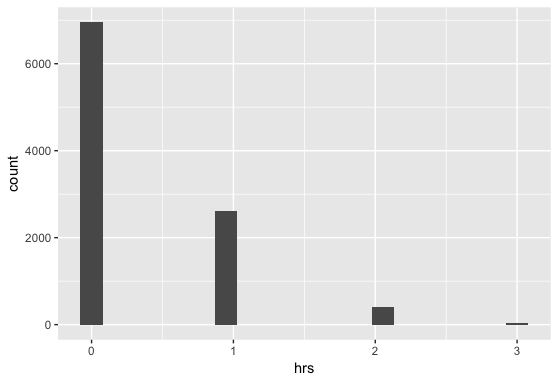
While Albert’s prediction now gives Stanton less than a 5% chance of reaching or breaking 61 (Maris’ record), he does have a 32% chance of reaching Ruth’s mark. That is, he has a 32% chance of hitting 1 home run today. You can see this clearly in histogram of Albert’s model.
Carpenter’s model echos this prediction fairly closely. The model updated to today:
ab <- 592
hr <- 59
games_played <- 158
games_remaining <- 1
phrs <- sum(rbinom(1e5,
rpois(1e5, games_remaining * ab / games_played),
rbeta(1e5, 1 + hr, 1 + ab - hr))
>= (61 - hr)) / 1e5
print(paste("Probability of tying or breaking the record:",
round(phrs, 3)))
[1] "Probability of tying or breaking the record: 0.057"
5.7% chance of catching Maris. Carpenter’s model also repeats Albert’s estimate of 31.4% that he will catch Babe Ruth.
We can but hope. As we say in Brazil, “esperança é a última a morrer” (Hope is the last thing to die).
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
