awalé
[This article was first published on Xi'an's Og » R, and kindly contributed to R-bloggers]. (You can report issue about the content on this page here)
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
 Following Le Monde puzzle #810, I tried to code an R program (not reproduced here) to optimise an awalé game but the recursion was too rich for R:
Following Le Monde puzzle #810, I tried to code an R program (not reproduced here) to optimise an awalé game but the recursion was too rich for R:
Error: evaluation nested too deeply: infinite recursion / options(expressions=)?
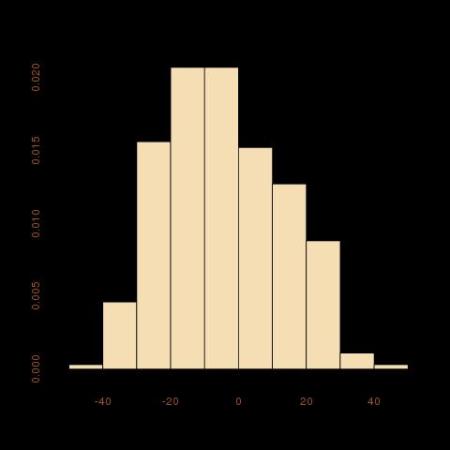
even with a very small number of holes and seeds in the awalé… Searching on the internet, it seems the computer simulation of a winning strategy for an awalé game still is an open problem! Here is a one-step R function that does not produce sure gains for the first player, far from it, as shown by the histogram below… I would need a less myopic strategy by iterating this function at least twice.
onemorestep=function(x,side){
# x current state of the awale,
# side side of the awale (0 vs 1)
M=length(x);N=as.integer(M/2)
rewa=rep(0,M)
newb=matrix(0,ncol=M,nrow=M)
for (i in ((1:N)+N*side)){
if (x[i]>0){
y=x
y[i]=0
for (t in 0:(x[i]-1))
y[1+(i+t)%%M]=y[1+(i+t)%%M]+1
last=1+(i+t)%%M
if (side){ gain=(last<=N)
}else{ gain=(last>N)}
if (gain){# ending up on the right side
rewa[i]=0
while (((last>0)&&(side))||((last>N)||(!side)))
if ((y[last]==2)||(y[last]==3)){
rewa[i]=rewa[i]+y[last];y[last]=0
last=last-1
}else{ break()}
}
newb[i,]=y
}
}
if (max(rewa)>0){
sol=order(-rewa)[1]
}else{ sol=rang=((1:N)+N*side)[x[((1:N)+N*side)]>0]
if (length(rang)>1) sol=sample(rang,1,prob=x[rang]^3)}
return(list(reward=max(rewa),board=newb[sol,]))
}
Filed under: Kids, pictures, R Tagged: awalé, infinite recursion, Le Monde, R
To leave a comment for the author, please follow the link and comment on their blog: Xi'an's Og » R.
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.