It is often very useful to practise mathematics by automatically generated exercises. One approach is multiple choice quizzes (MCQ), but it turns out to be fairly difficult to generate authentic wrong answers. Instead, we want the user to input the answer and be able to parse the answer and check ...

Box plots are often used. They are not always the best visualisation (e.g. is bi-modality not visible), but I will not discuss that in this post. Here, I will use it as an example of Importance sampling that is a technique to estimate tail probabi...

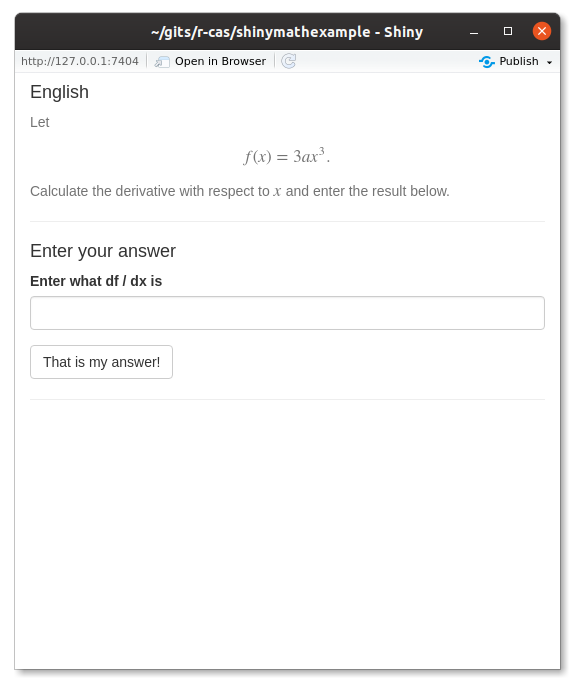
Finding prediction intervals (for future observations) is something different than finding confidence intervals (for unknown population parameters). Here, I demonstrate one approach to doing so. First we load the library and simulate some data:

library(mgcv)
set.seed(1)
dat <- gamSim(eg = 1, n = 400, dist = "normal", scale = 2)
## Gu & Wahba 4 term additive model

The simulated in dat contains the “truth” in the f variables:

str(dat)
## 'data.frame':    400 obs. of  10 variables:
##  $ y : num  3.3407 -0.0758 10.6832 8.7291 14.9911 ...
##  $ x0: num  0.266 0.372 0.573 0.908 0.202 ...
##  $ x1: num  0.659 0.185 0.954 0.898 0.944 ...
##  $ x2: num  0.8587 0.0344 0.971 0.7451 0.2733 ...
##  $ x3: num  0.367 0.741 0.934 0.673 0.701 ...
##  $ f : num  5.51 3.58 8.69 8.75 16.19 ...
##  $ f0: num  1.481 1.841 1.948 0.569 1.184 ...
##  $ f1: num  3.74 1.45 6.74 6.02 6.6 ...
##  $ f2: num  2.98e-01 2.88e-01 8.61e-05 2.16 8.40 ...
##  $ f3: num  0 0 0 0 0 0 0 0 0 0 ...
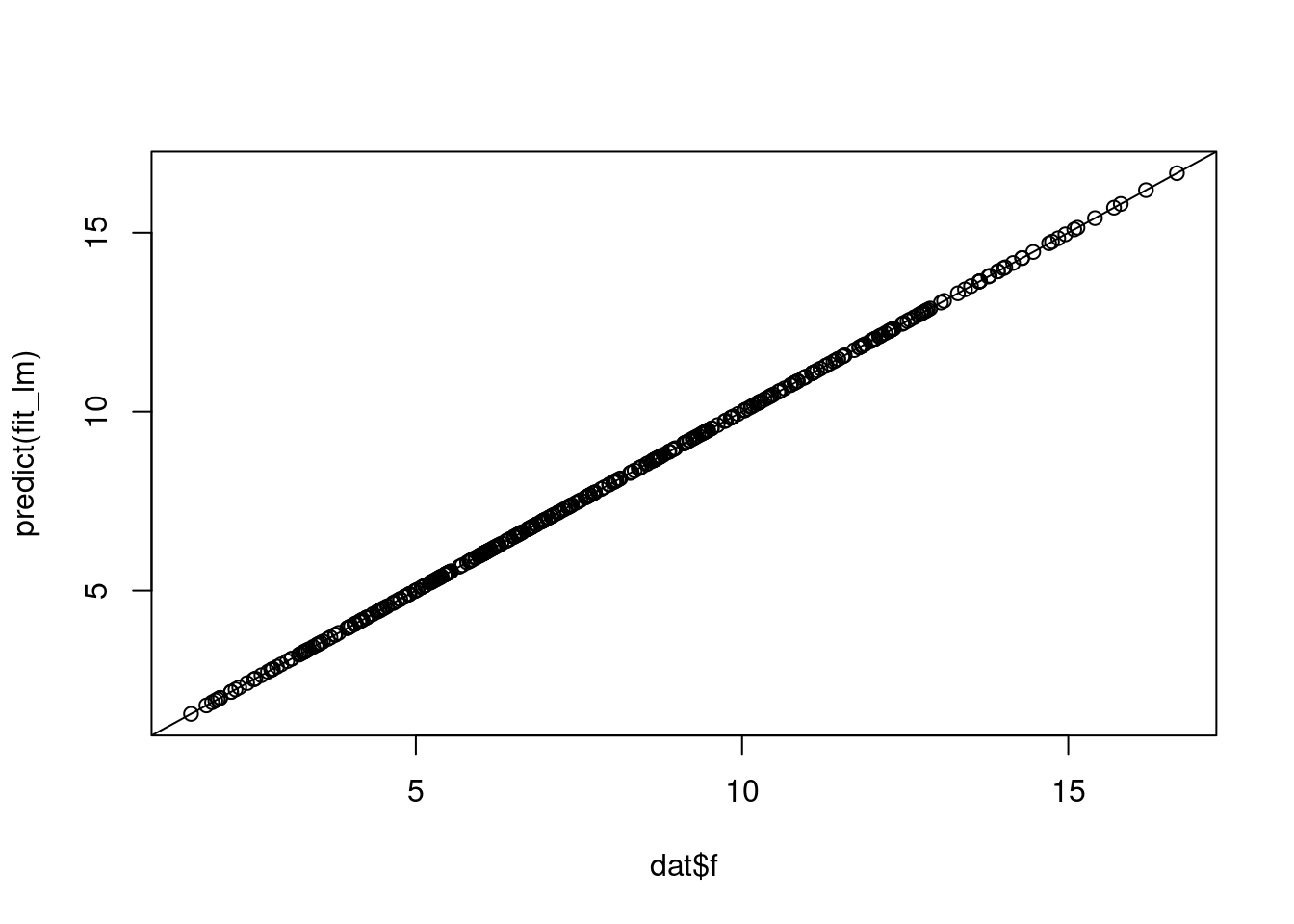
fit_lm <- lm(f ~ f0 + f1 + f2 + f3, data = dat)
plot(dat$f, predict(fit_lm))
abline(0, 1)

And what can ...

Let \(\rho_{XY}\) be the correlation between the stochastic variables \(X\) and \(Y\) and similarly for \(\rho_{XZ}\) and \(\rho_{YZ}\). If we know two of these, can we say anything about the third? In a recent blog post I dealt with the problem mathematically and I used the concept ...

Update Aug 10, 2019: I wrote a new blog post about the same as below but using a simulation approach. Update Aug 27, 2019: Minor change in how equations are solved (from version 0.9.0.9122). Let \(\rho_{XY}\) be the correlation between the stochastic variables \(X\) and \(Y\) and similarly for \(\rho_{XZ}\) and \(\rho_{YZ}\). ...

Update Aug 27, 2019: I wrote a new blog post showing that Ryacas can now solve the system of equations directly without using optim(). As you may know, I am maintaining the Ryacas package (with online documentation) for doing symbolic mathematics (and other stuff) in R using the yacas software (with online ...

I am learning how to play piano. In that process, I needed charts with piano chords. I know it is good practise to construct the chords manually, figure out the inversions and so on, but I found that some aspects of learning were improved with a chord chart. I searched ...