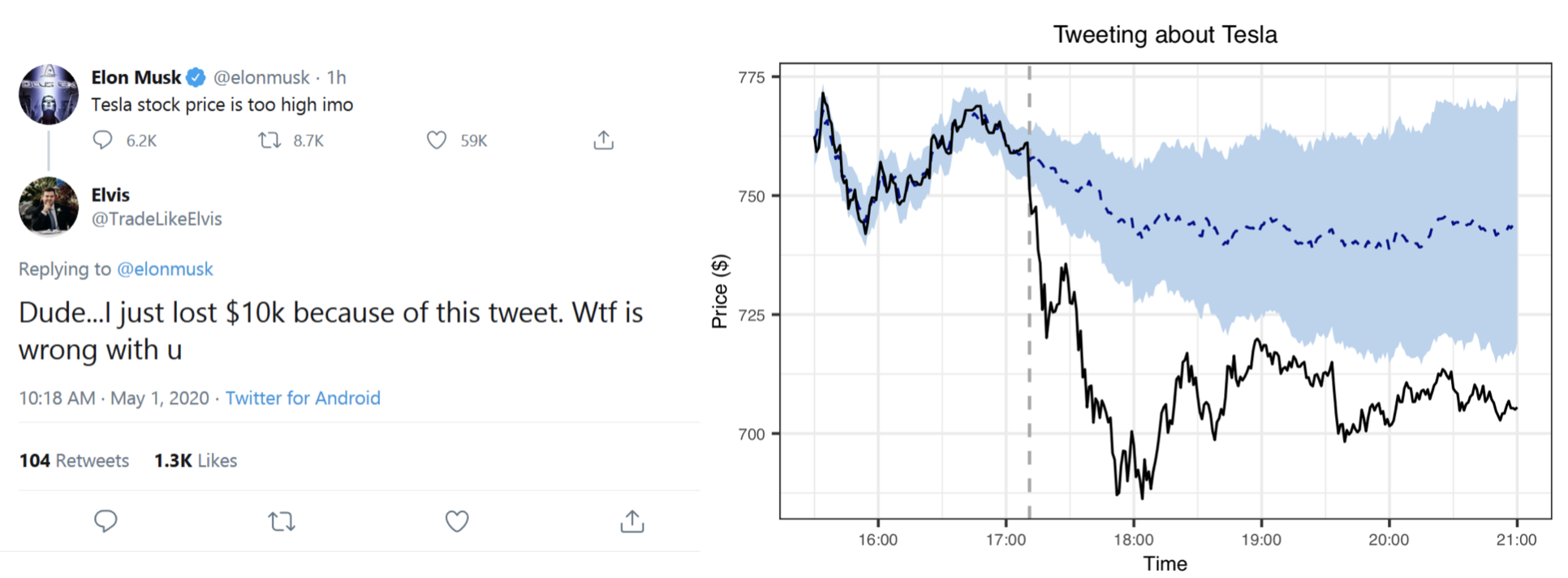
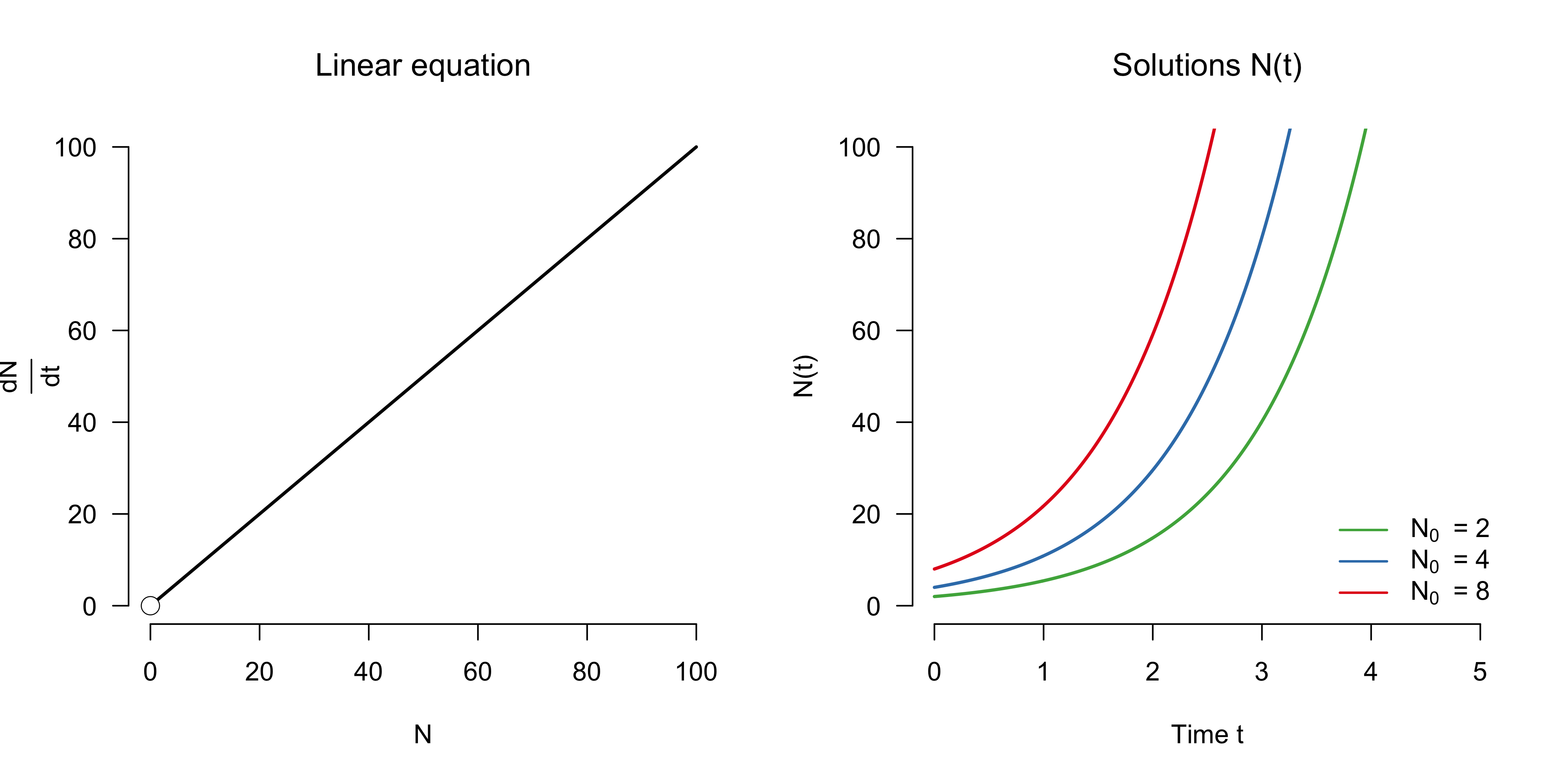
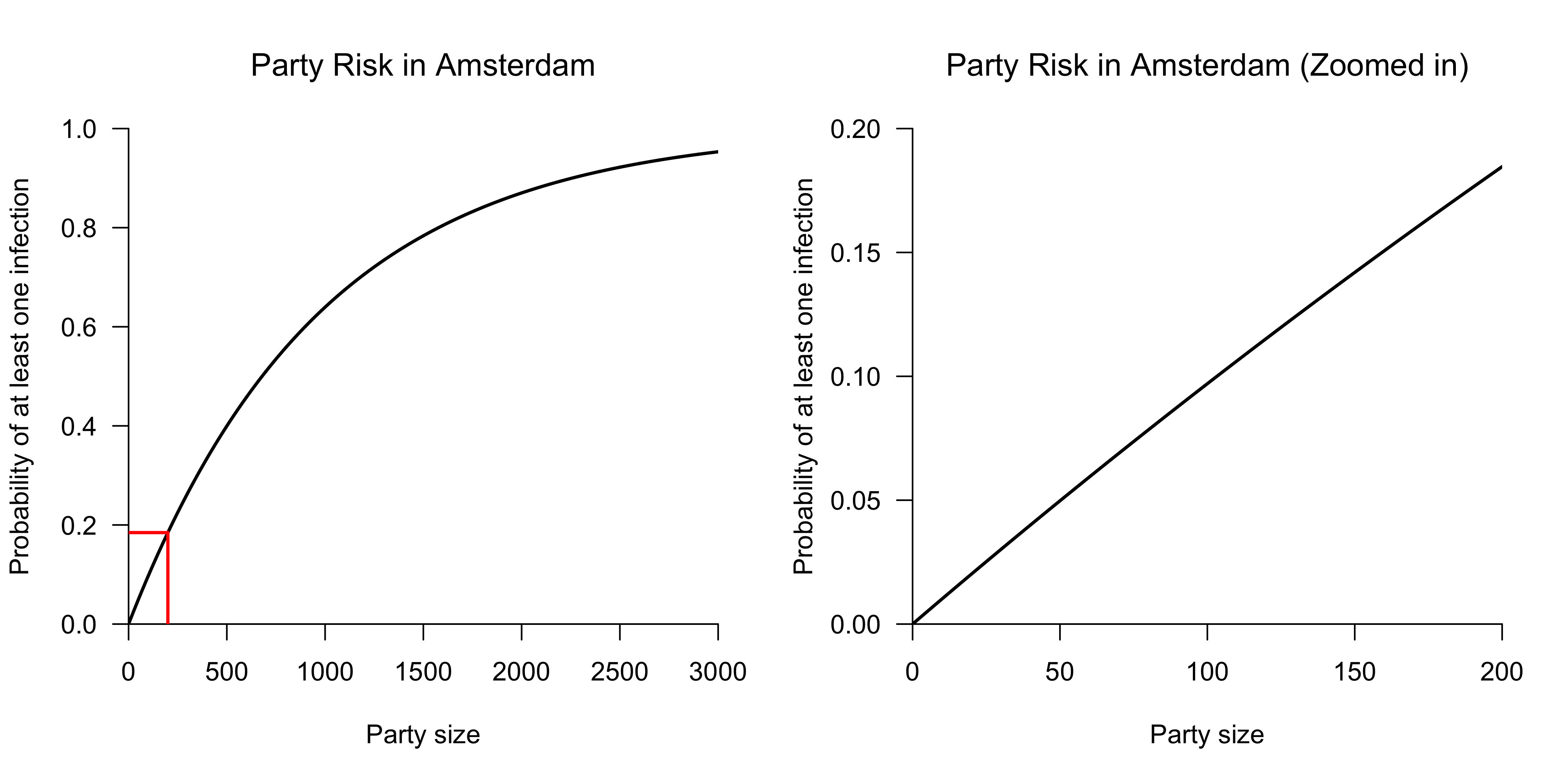
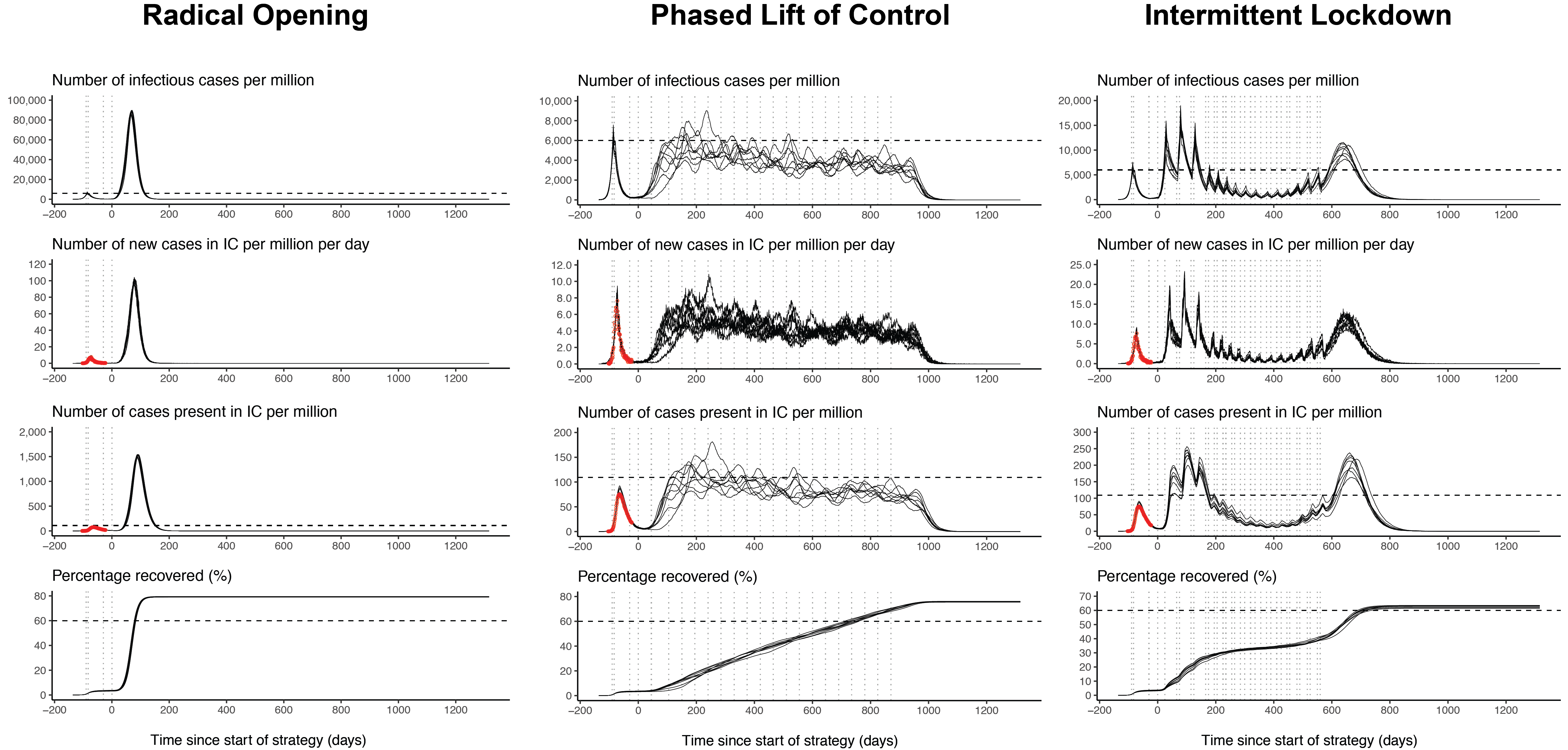
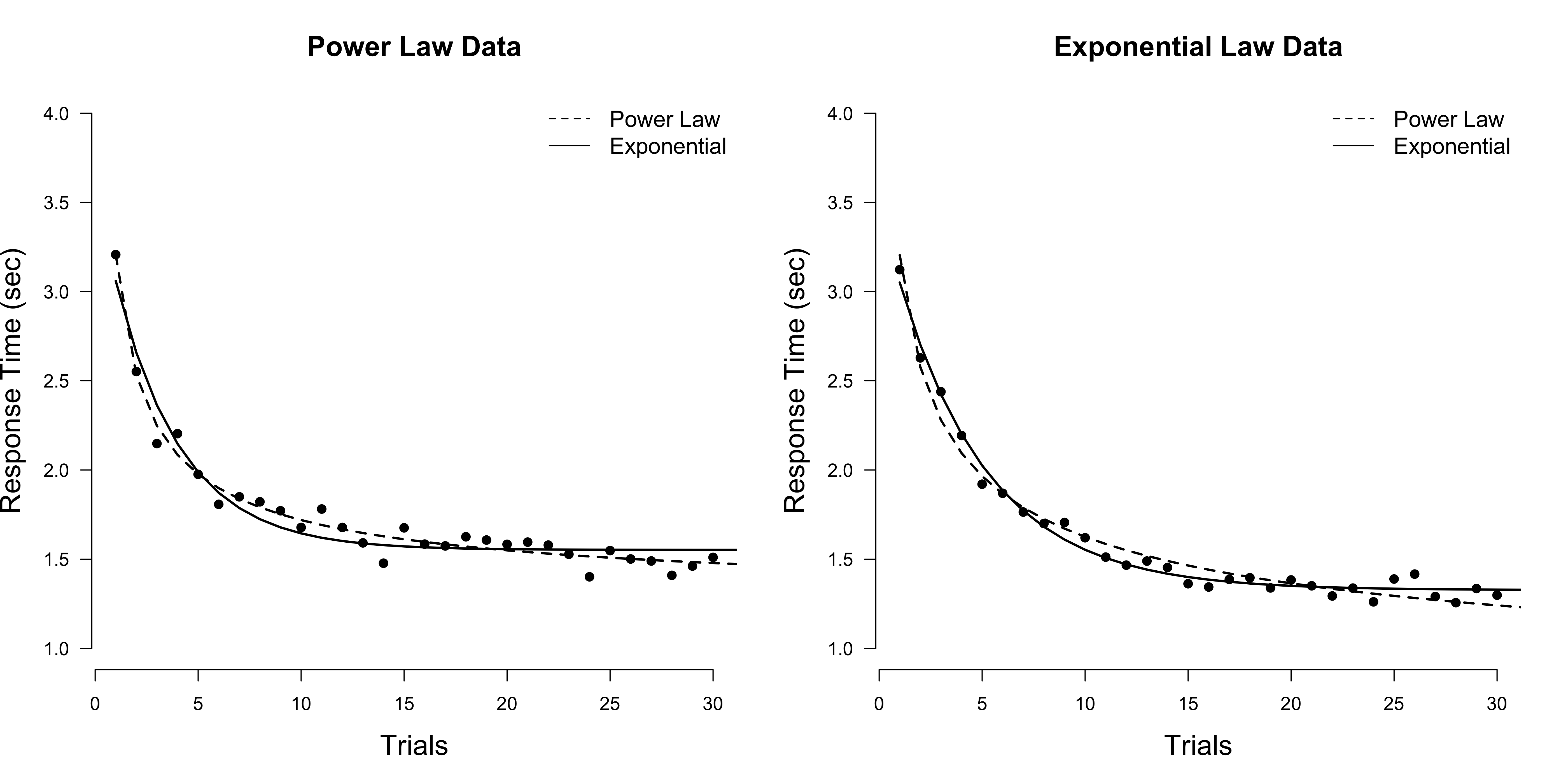
Causal effect of Elon Musk tweets on Dogecoin price
If you think of Dogecoin — the cryptocurrency based on a meme — you can’t help but also think of Elon Musk. That guy loves the doge, and every time he tweets about it, the price goes up. While we all know that correlation is not causation, we might s... [Read more...]