A bit more understanding of Cronbach’s alpha
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
Cronbach’s alpha reliability coefficient is one of the most widely used indicators of the scale reliability. It is used often without concern for the data (this will be a different text) because it is simple to calculate and it requires only one implementation of a single scale. The aim of this article is to provide some more insight into the functioning of this reliability coefficient without going into heavy mathematics. The main formula for the structure of variance is
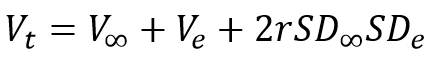
That is – the total variance is composed of the variance of the real results, the error variance and their covariance. Since the error is random and does not correlate with anything we can drop the covariance part of the formula. The reliability is by definition a ratio of the variance of real results and total variance and is usually represented with the symbol rxx. With this information we can reformulate the structure of the variance

Therefore to find out about the reliability, we are searching for the proportion of the error variance. Now to Cronbach’s alpha. The formula for alpha is
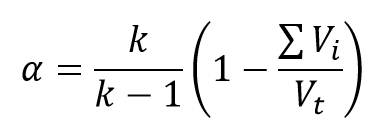
Let’s dissect this formula
In the first part we will concentrate on the rightmost part of this formula. The structure of the variance of any linear combination is a sum of variances of individual variables and double sum of covariances between the variables. If the intercorrelation between the variances is low, the test is not homogenous and the variance of the linear combination is composed mainly from the sum of the variances of individual variables. If the intercorrealtion is zero, the total variance is equal to the sum of variances of individual variables. The
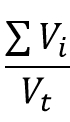
part gives us the information of how much of total variance is attributed to the sum of individual variances. This number has a maximum value of 1 and represents the situation when there is no intercorrelation between the variables. Therefore if we substract this from 1 we get the representation of the proportion of variance attributed to covariances of the individual variables.
To simplify things a bit, let’s work with standardized variables (M=0, V=1). In the formula for the variance of the linear combination
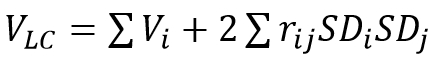
when we work with standardized variables, all individual variances are 1 so the formula can be replaced with
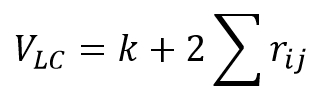
with k being the number of variables.
If the correlation between variables is 1 the number of correlations is k(k-1)/2 so the formula for the total variance would be

So to conclude, if the intercorrelations are zero VLC=k, and if the intercorrelations are 1, VLC=k2
Therefore the importance of the covariances within the total variance grows as the intercorrelations between items become higher, and when the number of items gets larger.
In the next part we can concentrate on the k/(k-1) part of the formula for alpha coefficient.
As we have seen in the previous part, the ratio of the sum of individual variances and the total variance is dependent on the intercorrelations between the items, but also on the number of items. If we would not correct this number, the maximum reliability would become dependent on the number of items and the scales with less items would be considered unreliable even if the intercorrelation is 1 between all items. Let’s see the example of a scale with two items with correlation 1 without the correction.

As the number of items becomes larger, this becomes less important since the importance of the number of items grows within the formula for the total variance. If the number of items is 100 and the intercorrelation is 1, this equation would give us 0.9. Therefore it is necessary to introduce the correction factor for the number of items that removes the penalization of the coefficient related to the number of items. The part k/(k-1) of the formula for alpha serves that purpose and since this part has a maximum value of 2 when the number of items is 2, and the minimum value of 1 when the number of items is infinite, it serves as the correction of the second part of the alpha formula.
To conclude, we have seen that the alpha coefficient is the simple way for measuring the homogeinity of a scale and that we can improve this coefficient by either using variables that have high correlation with other variables, or by adding more variables to the scale, or preferably – both.
The simulation in R
We will now use R to see what does the simulation of data show. We will create a set of standardized variables with a given intercorrelation and variate this intercorrealtion and the number of variables.
In the first part we have to load the packages
library(MASS) library(psych) library(ggplot2)
Now we will iterate through sets of n_var variables with t_cor intercorrelation. The minimum number of variables is 3 because R produces warning when calculating alpha on 2 variables when trying to calculate alpha if item deleted.
The results data frame has three columns that are necessary for plotting – intercorrelation, number of variables within the scale and the obtained alpha coefficient. For each intercorrelation we create 48 different scales with the number of items being from 3 to 50. To create results we use this code
res=data.frame() #the results data frame
step=0
for (t_cor in seq(from=0.1, to=0.9, by=0.2)){ #correlations go from 0.1 to 0.9
for (n_var in 3:50){ #number of variables goes from 3 to 50
rmat=diag(1,n_var) #create empty correlation matrix
for (i in 1:n_var){
for (j in 1:n_var) {
if (i!=j) {rmat[i,j]=t_cor} #fill the matrix with intercorrelations
}
}
mu <- rep(0,n_var) #create vector of means for variables
mat <- mvrnorm(100, Sigma = rmat, mu = mu, empirical = TRUE) #create variables using means and the correlation matrix
res[step+n_var-2,1]=t_cor #save target intercorrelation
res[step+n_var-2,2]=n_var #save number of variables in the scale
res[step+n_var-2,3]=psych::alpha(mat)$total$raw_alpha #save Cronbach's alpha
#both ggplot2 and psych packages have alpha function so it is explicitely declared
}
step=step+48 #this creates a new start for the next target intercorrelation
}
And finally we plot the data
ggplot(data = res, aes(x=V2, y=V3)) + geom_line(aes(colour=as.factor(V1)))+
xlab("Number of items")+
ylab("Alpha")+
labs(color="Intercorrelation")
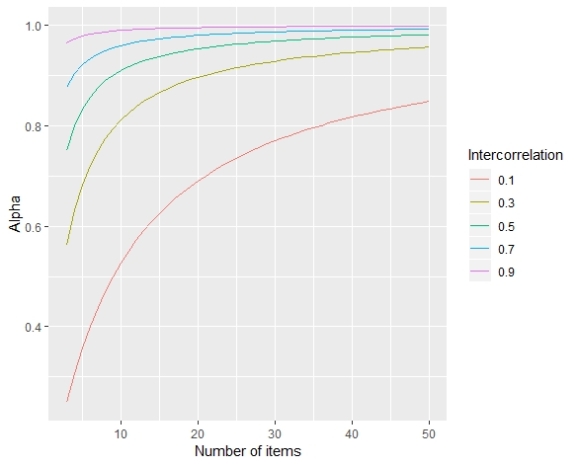
So what we see here is that the value of alpha coefficient indeed depends on the intercorrelation and the number of items in the scale. There is also a visible negative acceleration of the alpha coefficient as the number of items gets larger. The growth of alpha is quick at first, but as the number of items gets larger, the growth of alpha slows down.
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
