Gaussian clusters are found in a range of fields and simulating them is important as often we will want to test a given class discovery tools performance under conditions where the ground truth is known (e.g. K=6). However, a flexible Gaussian cluster simulator for simulating Gaussian clusters with defined variance, spacing, and size does not exist. This is why we made ‘clusterlab’, a new CRAN package (https://cran.r-project.org/web/packages/clusterlab/index.html). It was initially based on the Scikit-Learn make.blobs function, but now is much more sophisticated.

Clusterlab works in 2D space initially, because it is easy to work in mathematically. First, single 2D coordinates are placed on the perimeter of a circle by the algorithm, then they may be ‘pushed’ through vector multiplication with scalars outwards. Multiple rings of coordinates may be generated, this allows the user to create complex patterns through rotations of the individual rings. So by this point, we have the cluster center coordinates created in 2D space. Next, clusters are formed by adding Gaussian noise to the cluster centers and concatenating the new sample coordinates to our set of coordinates. Then, finally, to create high dimensional datasets these 2D coordinates are treated as principal component scores and projected into higher dimensions using fixed eigenvectors that are simulated again from a Gaussian distribution.

Let’s take a look at generating a six cluster dataset with clusterlab. The plots show the data in 2D principal component space.

library(clusterlab)
synthetic <- clusterlab(centers=6,centralcluster=TRUE)

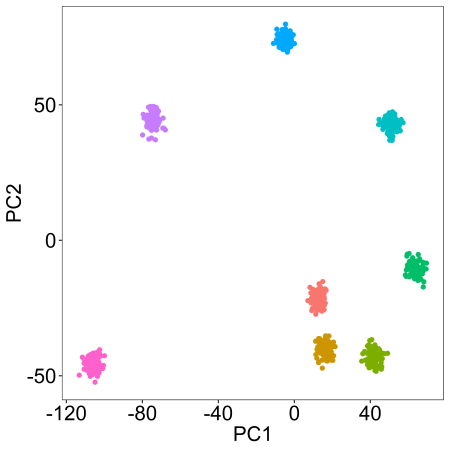
Next, we will change the variance of the clusters using the ‘sdvec’ parameter, this allows the user to set the variance of each cluster individually.

synthetic <- clusterlab(centers=6,sdvec=c(0.5,1,1.5,2,2,2))

We can also modify the ‘alpha’ parameter to push each cluster away from its central coordinate by a specified degree (a scalar) as follows:

synthetic <- clusterlab(centers=8,alphas=c(0,1,2,3,4,5,6,7))

Let’s also try simulating a more complex multi-ringed structure we talked about earlier. In this code we set the ‘ringthetas’ parameter to rotate the individual rings by a specified number of degrees (theta).

synthetic <- clusterlab(centers=5,r=7,sdvec=c(6,6,6,6,6),
alphas=c(2,2,2,2,2),centralcluster=FALSE,
numbervec=c(50,50,50,50),rings=5,ringalphas=c(2,4,6,8,10,12),
ringthetas = c(30,90,180,0,0,0), seed=123)

As a last demonstration, we will find the optimal K of the six cluster solution using the Bioconductor M3C package (https://www.bioconductor.org/packages/devel/bioc/html/M3C.html), which is a consensus clustering algorithm I use. We are going to use a smaller test dataset because I am on my laptop and it is quite old without many cores. And, we are going to set the Monte Carlo iterations parameter to 50 and use Ward’s hierarchical clustering because that should speed things up.

synthetic <- clusterlab(centers=6,centralcluster=TRUE,features=1000,
numbervec=c(30,30,30,30,30,30))
library(M3C)
d <- synthetic$synthetic_data
res <- M3C(d,iters=50,printres = TRUE,clusteralg = 'hc')

So as there is a maximal Relative Cluster Stability Index (RCSI) for K=6, M3C confirms our simulation. I think this is pretty neat. The clusterlab and M3C methods are described in our bioRxiv preprint (https://www.biorxiv.org/content/early/2018/07/25/377002).