This semester my studies all involve one key mathematical object: Gaussian processes. I’m taking a course on stochastic processes (which will talk about Wiener processes, a type of Gaussian process and arguably the most common) and mathematical finance, which involves stochastic differential equations (SDEs) used for derivative pricing, including in the Black-Scholes-Merton equation. Then I’m involved in a Gaussian process and stochastic calculus reading group. So these processes will take up a lot of my attention.

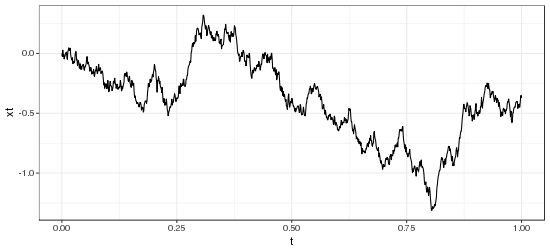
In a conversation about these processes with a fellow graduate student I was explaining the idea that different kernels (covariance functions, or ) define different Gaussian processes and simply changing the kernel will produce new processes with completely different properties. Let be the kernel of a process. is the kernel associated with the Wiener process and produces a process that is continuous everywhere but not differentiable anywhere, and with independent, Gaussian-distributed increments. 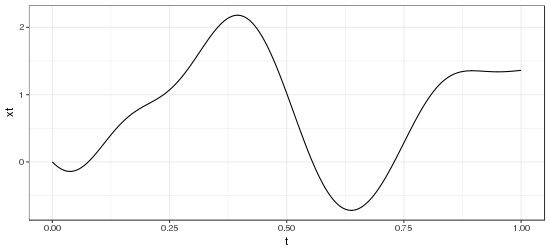On the other hand, the process defined by the kernel is not only continuous but differentiable everywhere, yet does not have independent increments.

I wanted to drive home the point that different kernels yield processes with wildly different properties by simulating and plotting them on a computer. So I whipped out the following R function in less than ten minutes (not counting documentation), and it does exactly what I want it to do.

library(MASS)

gaussprocess <- function(from = 0, to = 1, K = function(s, t) {min(s, t)},
                         start = 0, m = 1000) {
  # Simulates a Gaussian process with a given kernel
  #
  # args:
  #   from: numeric for the starting location of the sequence
  #   to: numeric for the ending location of the sequence
  #   K: a function that corresponds to the kernel (covariance function) of
  #      the process; must give numeric outputs, and if this won't produce a
  #      positive semi-definite matrix, it could fail; default is a Wiener
  #      process
  #   start: numeric for the starting position of the process
  #   m: positive integer for the number of points in the process to simulate
  #
  # return:
  #   A data.frame with variables "t" for the time index and "xt" for the value
  #   of the process
  
  t <- seq(from = from, to = to, length.out = m)
  Sigma <- sapply(t, function(s1) {
    sapply(t, function(s2) {
      K(s1, s2)
    })
  })
  
  path <- mvrnorm(mu = rep(0, times = m), Sigma = Sigma)
  path <- path - path[1] + start  # Must always start at "start"
  
  return(data.frame("t" = t, "xt" = path))
}

Below are example processes simulated by this function.

(Wiener process)

(Gaussian kernel)

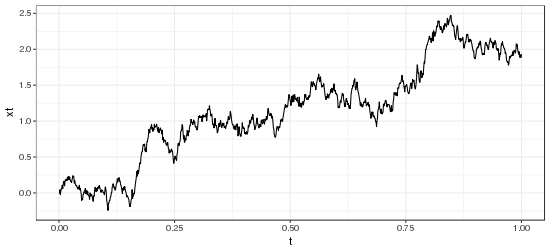
(Something completely different)

Hopefully you found this code snippet entertaining, if not useful.

I have created a video course published by Packt Publishing entitled Data Acqusition and Manipulation with Python, the second volume in a four-volume set of video courses entitled, Taming Data with Python; Excelling as a Data Analyst. This course covers more advanced Pandas topics such as reading in datasets in different formats and from databases, aggregation, and data wrangling. The course then transitions to cover getting data in “messy” formats from Web documents via web scraping. The course covers web scraping using BeautifulSoup, Selenium, and Scrapy. If you are starting out using Python for data analysis or know someone who is, please consider buying my course or at least spreading the word about it. You can buy the course directly or purchase a subscription to Mapt and watch it there.

If you like my blog and would like to support it, spread the word (if not get a copy yourself)! Also, stay tuned for future courses I publish with Packt at the Video Courses section of my site.