A Useful Logical Shortcut in R
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
While dealing with a small problem in which I needed a list of odd numbers, I remembered a shortcut that I’ve used for more than 30 years to reduce the typing and complication of logical tests — the “if…then” construct. I find this shortcut very useful.
Approach to Programming
It’s not elegant. However, my approach to programming in R (and other languages) is highly practical. I am a virologist, not a specialist in programming. I want my programs to work and work efficiently enough to accomplish the tasks I’ve set myself. However, the most concise and elegant code are normally not my goals. If a simple but brutish solution to a problem (using for loops and other antiquated concepts) works and runs in a reasonable time on my dataset, I don’t see the need to spend another three hours or so finding a more elegant solution. I would rather move onto the next problem and solve that.
With large datasets, I’m obviously more sensitive to the efficiency of the code and I will work harder and longer to get a solution that will do the calculations I need rapidly. In the study of viruses, many of our datasets are stupendously large–multiple gigabytes–and these get some really serious attention. Our lab is working on a study of histone methylation, which is exemplary of the efforts to find an efficient solution. Even before working through the dataset, we are testing various Bioconductor packages against other web-based and client software packages to find the most practical method to execute our analysis.
Preparation for the Shortcut
Before I show you the shortcut itself, we need to return to the set of odd numbers I want to create. What is the defining characteristic of an odd number we can use to separate them from even numbers? Simply, the odd numbers are not 0 nor divisible by 2. In R, we can use the modulus operator (“%%“) to determine if a number is divisible by 2. Let’s look at a little code because modulus is a concept that gives some people have a hard time.
Let’s first try some simple modulus arithmetic. We know that 4 is even (that is, it is divisible by 2) and 5 is not. Let’s see if the modulus operator distinguishes them:
4 %% 2 ## [1] 0 5 %% 2 ## [1] 1
If a number is even, it will have a 0 remainder after being divided by 2. An odd number (e.g., 5) will have a remainder of 1 after being divided by 2. If we create a logical test from this property, odd numbers will have the result TRUE and even numbers FALSE.
Let’s see how the logical test would work. Let’s first try an even number then an odd number.
27 %% 2 == 1 # test of the oddness of an odd number ## [1] TRUE 424 %% 2 == 1 # test of the oddness of an even number ## [1] FALSE
These values are logical in type as confirmed by checking the class (i.e., the type) of the statement.
class(27 %% 2 == 1) ## [1] "logical"
The Shortcut
We also know that R gives logical values a numerical equivalent: FALSE is treated as 0 and TRUE is treated as 1. This property of logical values in computer languages–and it’s almost universal across languages–enables us to perform a logical test on any number and multiply the result by that number. The result will either be 0 (if the logical test fails, that is gives the result FALSE) or the value of the number. We can see that in our examples so far.
27 * (27 %% 2 == 1) ## [1] 27 424 * (424 %% 2 == 1) ## [1] 0
The result is either the value of the odd number or 0 in the case of the even number.
Let’s put the shortcut to work on a set of integers that we will choose at random. First, we will use runif (the Uniform Distribution) to choose a set of 10 numbers. Then, we will apply the shortcut and find out the sum of the odd numbers we have in the set. So you can check the result, I’ll print the original 10 numbers and the set showing the value of the odd numbers.
set.seed(42) #so you can replicate my results numbers <- as.integer(runif(10, min = 3, max = 2000)) sum(numbers * (numbers %% 2 == 1)) ## [1] 8999 numbers ## [1] 1829 1874 574 1661 1284 1039 1473 271 1315 1411 (odd_nums <- numbers[numbers %% 2 == 1]) ## [1] 1829 1661 1039 1473 271 1315 1411 sum(odd_nums) ## [1] 8999
Alternative to the Shortcut
What is the shortcut equivalent to in R? The closest I can think of is a simple if conditional statement, which in our example would need to work with a for loop to calculate the sum:
odd_nums2 <- vector(mode = "integer")
for (i in seq_along(numbers)) {
if (numbers[i] %% 2 == 1) {
odd_nums2 <- c(odd_nums2, numbers[i])
}
}
odd_nums2
## [1] 1829 1661 1039 1473 271 1315 1411
sum(odd_nums2)
## [1] 8999
This produces an identical result. I could have programmed the sum within the for loop. However, I wanted you to be able to see the set of numbers themselves as well as the sum.
Put Shortcut to the Speed Test
Let’s now create a really big vector of numbers, say 50,000 numbers long and apply both versions of the algorithm to the set and see how long each takes to calculate. To do this, I will use the microbenchmark package. To make the microbenchmark timing work, I will convert both algorithms to functions. To make the comparison a bit more clear, microbenchmark will calculate the sum 100 times for each algorithm. For this comparison, I am going to have the for…if structure simply calculate the sum, not store the entire sequence of odd numbers. This will lose some information, but make the timing more comparable.
suppressPackageStartupMessages(library(microbenchmark))
suppressMessages(library(tidyverse))
## Shortcut function
shortcut <- function(numvec){
sum(numvec * (numvec %% 2 == 1))
}
## For...if structure function
forif <- function(numvec) {
sumodds <- 0
for (i in seq_along(numvec)) {
if (numvec[i] %% 2 == 1) {
sumodds <- sumodds + numvec[i]
}
}
return(sumodds)
}
# get vector of numbers
bigvec <- as.integer(runif(50000, min = 3, max = 2000))
## calculate sum of odd numbers with shortcut
paste("Shortcut Total =", shortcut(bigvec))
## [1] "Shortcut Total = 25198126"
## calculate the sum of odd numbers with the for...if structure
paste("For...if Total =", forif(bigvec))
## [1] "For...if Total = 25198126"
## calculate the timing
res <- microbenchmark(shortcut(bigvec), forif(bigvec), times = 100L)
print(res)
## Unit: milliseconds
## expr min mean median max
## shortcut(bigvec) 1.372 2.052 1.923 3.722
## forif(bigvec) 14.191 19.036 18.021 34.338
print(res, unit = "relative")
## Unit: relative
## expr min mean median max
## shortcut(bigvec) 1.000 1.000 1.000 1.000
## forif(bigvec) 10.342 9.277 9.369 9.226
suppressMessages(autoplot(res) +
scale_y_continuous(breaks = seq(0, 36, by = 4)) +
ylab("Time in milliseconds"))
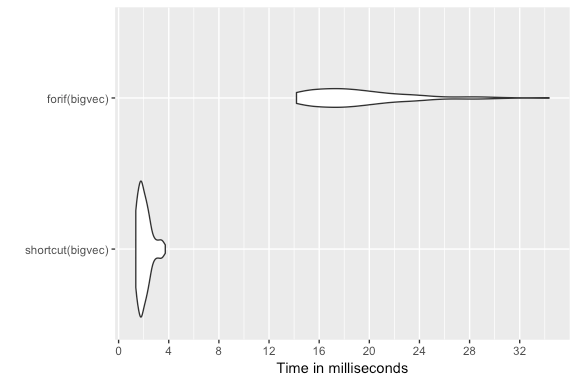
As you can see from the graph and the results, the shortcut saves considerable processing time. One important reason for this is that it can take advantage of R’s inherent vectorization. It can process each value in the set without having to construct a loop and test each value in a separate command. The shortcut provides approximately a 9.3 times speed advantage in processing a vector of 50,000 values.
Conclusion
We can summarize the shortcut by the following expression:
Result of logical test * numerical value
The shortcut can be used with any expression that produces a logical value (TRUE/FALSE). It can also be applied to any numerical value. For example, if I wanted to calculate the price of a ticket to a show for an elderly person in a city where persons over 65 years of age receives a discount of 30%, I could use the following expression in R:
(age > 65) * 0.30
We can now use this shortcut to calculate a ticket price for two people, one above 65 and one younger.
ages <- c(67, 45) discount <- .30 full_price <- 40 prices <- (1 - (ages > 65) * discount) * full_price prices ## [1] 28 40
As you can see, the 67 year old received the discount, the younger person did not. Try using this in your programming. Once you begin to apply it, you will find it a handy tool.
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
