Who Survives Riddler Nation?
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
Introduction
Last week, I published an article on learning to fight in the Battle for Riddler Nation. Here’s a refresher of the rules:
In a distant, war-torn land, there are 10 castles. There are two warlords: you and your archenemy. Each castle has its own strategic value for a would-be conqueror. Specifically, the castles are worth 1, 2, 3, …, 9, and 10 victory points. You and your enemy each have 100 soldiers to distribute, any way you like, to fight at any of the 10 castles. Whoever sends more soldiers to a given castle conquers that castle and wins its victory points. If you each send the same number of troops, you split the points. You don’t know what distribution of forces your enemy has chosen until the battles begin. Whoever wins the most points wins the war.
Submit a plan distributing your 100 soldiers among the 10 castles. Once I receive all your battle plans, I’ll adjudicate all the possible one-on-one match-ups. Whoever wins the most wars wins the battle royale and is crowned king or queen of Riddler Nation!
This battle took place in two rounds. In the first round, I submitted the solution (1, 1, 1, 1, 1, 1, 23, 23, 24, 24) using intuition, and did not do particularly well. In the second round, I used agent-based modelling and an evolutionary model to get a solution. The strategy (3, 3, 13, 2, 4, 1, 27, 30, 10, 7), performed best in the last round of the simulated 100-years war of Riddler Nation, so I submitted it to the contest.
The results of the second round are now out, and although Mr. Roeder enjoyed my article enough to give it a shout-out (sweet, my name is on FiveThirtyEight, which is among my favorite news sites!), I did not win. Now, this is not shocking; with 931 participants, and game theory essentially reducing every game to either domination by one player or an optimal gamble (the latter being true here), the chances of my coming out on top are slim. With that in mind, I cannot be disappointed. In fact, I have some reasons to feel good; my strategy beats the top performers, who seemed to expect others would play the optimal strategy from the first round (Mr. Roeder’s statistics revealed a downward shift in troop allocations to lower-valued castles) and thus chose a strategy to beat it. Perhaps my strategy was ahead of its time? Who knows.
Mr. Roeder has published the strategies his readers submitted for the second round, and I will be rebuilding a strategy from that data using Mesa and agent-based modeling again, but we will be doing more.
First, let’s see how well my strategy did in the last round, because I want to know.
Second, I’m going to explore the idea that my method generates a mixture of strategies that reflects the game-theoretic optimal strategy. (See the conclusion of my previous post to see the definition of this strategy and its properties.) In some sense, this allows me to determine if I lost the last round because of bad luck or because other players were choosing superior strategies.
Third, I want to cluster the strategies so I can see what “species” of strategies people chose. I use the excellent R package mclust for this clustering.
Fourth and finally, I visualize the evolution of strategies as my simulation plays out, using ggplot2, dimensionality reduction, and gganimate.
Results of the Last Battle for Riddler Nation
The winning strategy of the last round, submitted by Vince Vatter, was (0, 1, 2, 16, 21, 3, 2, 1, 32, 22), with an official record1 of 751 wins, 175 losses, and 5 ties. Naturally, the top-performing strategies look similar. This should not be surprising; winning strategies exploit common vulnerabilities among submissions.
I’ve downloaded the submitted strategies for the second round (I already have the first round’s strategies). Lets load them in and start analyzing them.
import pandas as pd
from pandas import Series, DataFrame
import numpy as np
from numpy.random import poisson, uniform
import mesa, mesa.time, mesa.datacollection
import pymysql, sqlalchemy
import random
# Code from the last post
def gen_strat(obj):
"""Generating a Series consisting of castle troop assignments
args:
obj: An iterable (NumPy array, Series, list, tuple, etc.) containing troop assignment
return:
Series; The generated strategy
"""
srs = Series(obj).apply(int)
if (len(srs) != 10) or (srs.sum() != 100) or ((srs < 0).values.any()):
raise ValueError("A valid strategy consists of ten integers between 0 and 100 that sum to 100.")
srs.index = pd.Index(np.arange(10) + 1)
return srs
def check_strat(strat):
"""Checks that strat is a valid strategy, like that created by gen_strat
args:
strat: Series; An object to check
return:
bool; True if valid
"""
if str(type(strat)) == "<class 'pandas.core.series.Series'>":
# All the other conditions that must hold
if len(strat) == 10 and strat.sum() == 100 and (strat >= 0).values.all() and \
(strat == strat.apply(int)).values.all() and (strat.index.values == (np.arange(10) + 1)).all():
return True
return False
def battle_strat(strat1, strat2):
"""Determine which strategy between two wins
args:
strat1: Series; generated by gen_strat (or obeying its rules)
strat2: Series; generated by gen_strat (or obeying its rules)
return:
dict; with the following fields:
* "winner": int; 1 for strat1, -1 for strat2, 0 for tie
* "pts": list; Item 0 is strat1's points, Item1 strat2's points
"""
if not check_strat(strat1) or not check_strat(strat2):
raise ValueError("Both strat1 and strat2 must be valid strategies")
castle_margins = strat1 - strat2
win1 = (castle_margins > 0).apply(int)
win2 = (castle_margins < 0).apply(int)
tie = (castle_margins == 0).apply(int)
castle_points = Series(strat1.index, index=strat1.index)
tie_pts = (tie * castle_points).sum() / 2
pts1 = (win1 * castle_points).sum() + tie_pts
pts2 = (win2 * castle_points).sum() + tie_pts
pts_list = [pts1, pts2]
if pts1 > pts2:
return {"winner": 1, "pts": pts_list}
elif pts1 < pts2:
return {"winner": -1, "pts": pts_list}
else:
return {"winner": 0, "pts": pts_list}
def battle_strat_df(df1, df2):
"""Adjudicate all battles to see who wins
args:
df1: DataFrame; A data frame of warlords' strategies
df2: DataFrame; A data frame of warlords' strategies
return:
DataFrame; Contains columns for Win, Tie, and Lose, the performance of the warlords of df1 against those
of df2
"""
df1_mat = df1.values
df2_mat = df2.values
score_mat = np.ones(df2_mat.shape, dtype=np.int8)
res = list()
for i in range(df1_mat.shape[0]):
vec = df1_mat[i, np.newaxis, :]
margin = vec - df2_mat
df1_castles = (margin > 0) * (np.arange(10) + 1)
df2_castles = (margin < 0) * (np.arange(10) + 1)
tie_castles = (margin == 0) * (np.arange(10) + 1)
tie_scores = tie_castles.sum(axis=1) / 2
df1_scores = df1_castles.sum(axis=1) + tie_scores
df2_scores = df2_castles.sum(axis=1) + tie_scores
res.append({"Win": (df1_scores > df2_scores).sum(),
"Tie": (df1_scores == df2_scores).sum(),
"Losses": (df1_scores < df2_scores).sum()})
return DataFrame(res, index=df1.index)
###########################
## Definition of the ABM ##
###########################
class Warlord(mesa.Agent):
"""A warlord of Riddler Nation, who starts with a war doctrine, provinces, and fights other warlords"""
def __init__(self, model, unique_id, doctrine, provinces, max_provinces, mutate_prob, mutate_amount):
"""Create a warlord
args:
model: mesa.Model; The model to which the agent belongs
unique_id: int; Identifies the agent
doctrine: Series; Describes the doctrine, and must be like one generated by gen_strat()
provinces: int; The number of provinces the warlord starts with
max_provinces: int; The maximum number of provinces a warlord can have before a split
mutate_prob: float; A number between 0 and 1 that represents the probability of a mutation in offspring
mutate_ammount: float; A number greater than 0 representing average number of mutations in doctrine
of offspring
return:
Warlord
"""
self.model = model
if not check_strat(doctrine):
raise ValueError("doctrine must be a valid strategy")
self.doctrine = doctrine
self.unique_id = int(unique_id)
self.provinces = max(0, int(provinces)) # provinces at least 0
self.max_provinces = max(2, int(max_provinces)) # max_provinces at least 2
self.mutate_prob = max(min(mutate_prob, 1), 0) # between 0 and 1
self.mutate_amount = max(mutate_amount, 0)
self.opponent = None # In future, will be the id of this warlord's opponent
def step(self):
"""In a step, find a new opponent to battle if not assigned"""
if self.opponent is None:
other = self.model.get_random_warlord()
self.opponent = other
other.opponent = self
def advance(self):
"""Fight, and handle death or split of provinces"""
if self.opponent is not None:
# Resolve battle
other = self.opponent
res = battle_strat(self.doctrine, other.doctrine)["winner"]
self.provinces += res
other.provinces -= res
# Clear opponents
self.opponent = None
other.opponent = None
# Resolve possible death
if self.provinces <= 0:
self.model.schedule.remove(self)
# If too many provinces, split, create new warlord
if self.provinces >= self.max_provinces:
son_doctrine = self.doctrine
son_mutate_prob = self.mutate_prob
son_mutate_amount = self.mutate_amount
son_provinces = int(self.provinces / 2)
# Is there a mutation?
if uniform() < self.mutate_prob:
# Yes! Apply the mutation
son_mutate_prob = (self.mutate_prob + 1) / 2
son_mutate_amount = self.mutate_amount * 2
# Change doctrine
mutations = min(poisson(self.mutate_amount), 100)
for _ in range(mutations):
son_doctrine[random.choice(son_doctrine.index)] += 1 # Add 1 to a random castle
son_doctrine[random.choice(son_doctrine[son_doctrine > 0].index)] -= 1 # Subtract 1 from a random
# castle that has at least
# one soldier
# Create the son
son = Warlord(model = self.model,
unique_id = self.model.next_id(),
doctrine = son_doctrine,
provinces = son_provinces,
max_provinces = self.max_provinces,
mutate_prob = son_mutate_prob,
mutate_amount = son_mutate_amount)
self.model.schedule.add(son)
# Changes to the warlord
self.mutate_prob /= 2
self.mutate_amount /= 2
self.provinces = self.max_provinces - son_provinces
class RiddlerBattle(mesa.Model):
"""The Model that handles the simulation of the Battle for Riddler Nation"""
def __init__(self, doctrines, N=None, max_provinces=6, mutate_prob=0.9, mutate_amount=10, debug=False):
"""Create an instance of the Battle for Riddler Nation
args:
doctrines: DataFrame; Contains all the doctrines for the warlords to create
N: int; The number of warlords to create; if None, the number of rows of doctrines
max_provinces: int; The maximum number of provinces each warlord can have
mutate_prob: float; Each warlord's initial mutation probability
mutate_amount: float; Each warlord's initial rate of number of mutations
debug: bool; Debug mode
return:
RiddlerBattle
"""
if N is None:
N = doctrines.shape[0]
if debug:
strat = {"Doctrine": lambda w: w.doctrine.values, "Provinces": lambda w: w.provinces}
else:
strat = {"Doctrine": lambda w: w.doctrine.values}
self.schedule = mesa.time.SimultaneousActivation(self) # Battles are determined simultaneously
self._max_id = 0 # The highest id currently used by the model
self.dc = mesa.datacollection.DataCollector(agent_reporters=strat) # Data collection
self.create_warlords(doctrines, N, max_provinces, mutate_prob, mutate_amount)
self._gen_warlord_list()
def create_warlords(self, doctrines, N, max_provinces, mutate_prob, mutate_amount):
"""Populate the model with warlords
args:
doctrines: DataFrame; Contains all the doctrines for the warlords to create
N: int; The number of warlords to create
max_provinces: int; The maximum number of provinces each warlord can have
mutate_prob: float; Each warlord's initial mutation probability
mutate_amount: float; Each warlord's initial rate of number of mutations
"""
i = 0
init_provinces = int(max_provinces / 2)
for _ in range(N):
w = Warlord(model = self,
unique_id = self.next_id(),
doctrine = doctrines.iloc[i, :],
provinces = init_provinces,
max_provinces = max_provinces,
mutate_prob = mutate_prob,
mutate_amount = mutate_amount)
self.schedule.add(w)
i += 1
if (i >= doctrines.shape[0]):
i = 0 # We've run out of available doctrines, so start at the beginning of the DataFrame
def _gen_warlord_list(self):
"""Generate a list of warlords used for assigning opponents"""
self._warlord_list = [w for w in self.schedule.agents]
def get_random_warlord(self):
"""Pull a random warlord without an opponent"""
i = random.choice([i for i in range(len(self._warlord_list))])
return self._warlord_list.pop(i)
def next_id(self):
"""Get the next valid id for the model, and update the max id of the model
return:
int; Can be used as an id
"""
self._max_id += 1
return self._max_id
def step(self):
"""Take a step"""
self.dc.collect(self)
self.schedule.step()
self._gen_warlord_list() # Reset the list of available warlords
def run_model(self, steps):
"""Run the model
args:
steps: int; The number of steps to run the model
"""
steps = int(steps)
for _ in range(steps):
self.step()
# Read in data, and create a DataFrame containing the strategies from both rounds
rs1 = pd.read_csv("castle-solutions.csv", encoding='latin-1').iloc[:, 0:10].applymap(int)
rs1.columns = pd.Index(np.arange(10) + 1)
rs1 = rs1.loc[rs1.apply(check_strat, axis=1), :] # Use only valid strategies
rs1.index = pd.Index(np.arange(rs1.shape[0]))
rs2 = pd.read_csv("castle-solutions-2.csv", encoding='latin-1').iloc[:, 0:10].applymap(int)
rs2.columns = rs1.columns.copy()
rs2 = rs2.loc[rs2.apply(check_strat, axis=1), :] # Use only valid strategies
rs2.index = pd.Index(np.arange(rs2.shape[0]))
# Combine into one DataFrame, with a multi-index for distinguishing participants
riddler_strats = pd.concat([rs1, rs2])
riddler_strats.index = pd.MultiIndex(levels=[[1, 2],
list(set(rs1.index.values.tolist()).union(rs2.index.values.tolist()))],
labels=[([0] * rs1.shape[0]) + ([1] * rs2.shape[0]),
rs1.index.values.tolist() + rs2.index.values.tolist()],
names=["round", "idx"])
riddler_strats.head()
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| round | idx | ||||||||||
| 1 | 0 | 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 52 | 2 | 2 | 2 | 2 | 2 | 2 | 12 | 12 | 12 | |
| 2 | 26 | 26 | 26 | 16 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 3 | 25 | 0 | 0 | 0 | 0 | 0 | 0 | 25 | 25 | 25 | |
| 4 | 25 | 0 | 0 | 0 | 0 | 0 | 0 | 25 | 25 | 25 |
del rs1, rs2 # No longer needed
Let’s see how my strategy fared.
# See how my strategy did in the second round myStrat = gen_strat((3, 3, 13, 2, 4, 1, 27, 30, 10, 7)) myStrat_vs_r2 = battle_strat_df(DataFrame([myStrat]), riddler_strats.loc[2]) myStrat_vs_r2
| Losses | Tie | Win | |
|---|---|---|---|
| 0 | 358 | 10 | 534 |
myStrat_vs_r2.Win / myStrat_vs_r2.values.sum() 0 0.592018 Name: Win, dtype: float64
You may recall that with my first strategy I was winning 48% of my battles, and now I won 59% of battles, an improvement.
Let’s now get an overall ranking for the round 2 strategies.
r2_res = battle_strat_df(riddler_strats.loc[2], riddler_strats.loc[2])
r2_res.sort_values("Win", ascending=False).head()
| Losses | Tie | Win | |
|---|---|---|---|
| idx | |||
| 0 | 169 | 6 | 727 |
| 1 | 179 | 9 | 714 |
| 2 | 182 | 8 | 712 |
| 4 | 193 | 6 | 703 |
| 3 | 194 | 10 | 698 |
This is an exact match to Mr. Roeder’s results (there’s one extra tie than there should be, since a strategy always ties against itself), which is good news. (It shows I’m not crazy!)
How did second-round strategies fare against the first?
r2_vs_r1 = battle_strat_df(riddler_strats.loc[2], riddler_strats.loc[1])
r2_vs_r1.sort_values("Win", ascending=False).head()
| Losses | Tie | Win | |
|---|---|---|---|
| idx | |||
| 299 | 107 | 4 | 1238 |
| 400 | 107 | 4 | 1238 |
| 300 | 107 | 4 | 1238 |
| 297 | 107 | 4 | 1238 |
| 379 | 108 | 3 | 1238 |
I would also like to summarize the strategies in round 2. One way is to take the mean of the troop allocations.
riddler_strats.loc[2].mean().round(0)
1 3.0
2 4.0
3 6.0
4 8.0
5 10.0
6 12.0
7 14.0
8 17.0
9 14.0
10 12.0
dtype: float64
# How did my strategy fair against the mean?
battle_strat(myStrat, gen_strat(riddler_strats.loc[2].mean().round(0)))
{'pts': [18.5, 36.5], 'winner': -1}
Strange… my strategy does not beat the mean strategy.
Mixed Strategy
Unfortunately, I did not save the data I generated from the last post; it’s gone forever. Below, I recreate the simulation I developed on the data from the first Battle for Riddler Nation. Furthermore, because I want to use this data later, I save the simulations in a MySQL database.
%time rb1 = RiddlerBattle(riddler_strats.loc[(1), :])
CPU times: user 3.42 s, sys: 32 ms, total: 3.45 s
Wall time: 3.56 s
%time rb1.run_model(100)
CPU times: user 17min 44s, sys: 1.83 s, total: 17min 46s
Wall time: 18min 9s
warlords1 = rb1.dc.get_agent_vars_dataframe()
warlords1 = DataFrame([w[1]["Doctrine"] for w in warlords1.iterrows()], columns=np.arange(10) + 1,
index=warlords1.index)
def pymysql_sqlalchemy_stringgen(user, passwd, host, dbname):
"""Generate a connection string for use with SQLAlchemy for MySQL and PyMySQL connections
Args:
user (str): The username of the connecting user
passwd (str): The user's password
host (str): The host for where the database is located
dbname (str): The name of the database to connect with
Returns:
(str) A SQLAlchemy connection string suitable for use with create_engine()
Additional options for the connection are not supported with this function.
"""
return "mysql+pymysql://" + user + ":" + passwd + "@" + host + "/" + dbname
conn = sqlalchemy.create_engine(pymysql_sqlalchemy_stringgen("root", pswd, "localhost", "riddlerbattles")).connect()
try:
conn.execute("DROP TABLE round1simulation;")
except:
pass
make_table = """CREATE TABLE `round1simulation` (
`step` int(4),
`agentid` int(8),
`castle_1` int(8),
`castle_2` int(8),
`castle_3` int(8),
`castle_4` int(8),
`castle_5` int(8),
`castle_6` int(8),
`castle_7` int(8),
`castle_8` int(8),
`castle_9` int(8),
`castle_10` int(8),
PRIMARY KEY (`step`,`agentid`)
);"""
conn.execute(make_table)
<sqlalchemy.engine.result.ResultProxy at 0xa979946c>
# Put the data in the table
temp_table = warlords1.copy()
temp_table.columns = pd.Index(["castle_" + str(i) for i in temp_table.columns])
temp_table.columns
Index(['castle_1', 'castle_2', 'castle_3', 'castle_4', 'castle_5', 'castle_6',
'castle_7', 'castle_8', 'castle_9', 'castle_10'],
dtype='object')
temp_table.to_sql("round1simulation", con=conn, if_exists='append')
del temp_table # Not needed any longer
As mentioned in my previous post, the optimal strategy is a random strategy. No choice of troop allocation that always win against other allocations exists. Instead, a player employing optimal play randomly allocates troops to castles, with some probability distribution. The question is: what is that probability distribution?
I hypothesize that the distribution of pure strategies used by the warlords generated by the ABM is close to whatever the optimal distribution is. In particular, random warlords picked from the final population of warlords produced by the ABM tie or beat random strategies picked by players at least half of the time.
I test this hypothesis below.
def random_battle(df1, df2):
"""Pick a random warlord from df1 and have him battle a random warlord from df2
Args:
df1: DataFrame; A data frame of warlords' strategies
df2: DataFrame; A data frame of warlords' strategies
Returns:
int; The result of the battle, with 1 for victory for the warlord from df1, -1 for defeat, 0 for tie
"""
return battle_strat(gen_strat(df1.sample(n=1).values[0]), gen_strat(df2.sample(n=1).values[0]))['winner']
warlords1.head()
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Step | AgentID | ||||||||||
| 0 | 1 | 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 52 | 2 | 2 | 2 | 2 | 2 | 2 | 12 | 12 | 12 | |
| 3 | 26 | 26 | 26 | 16 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 4 | 24 | 0 | 0 | 0 | 0 | 2 | 0 | 22 | 27 | 25 | |
| 5 | 26 | 0 | 0 | 0 | 0 | 1 | 0 | 24 | 25 | 24 |
# Do 1000 random battles, picking from my warlords found with the ABM and those from the second round of the # Battle for Riddler Nation rand1 = Series([random_battle(warlords1.loc[99], riddler_strats.loc[2]) for _ in range(1000)]) rand1.head() 0 -1 1 1 2 -1 3 -1 4 -1 dtype: int64 rand1.value_counts() -1 508 1 469 0 23 dtype: int64 # Winning proportion rand1.value_counts().loc[1] / rand1.value_counts().sum() 0.46899999999999997
That is not good news for my hypothesis. The strategies found via the ABM lose against human opponents more frequently than they win. This should not be happening if my belief were correct.
Perhaps ABMs cannot be used to solve this problem after all, or at least for my approach. Then again, maybe I need a longer “training” period; that is, 100 rounds are not enough to learn a strategy. Perhaps 1,000 or 3,000 are needed (though completing that many round would take a long time), or I need to seed the system with more agents.
Strategy Clusters
I believe that humans are going to be prone to choosing strategies that follow similar themes. Perhaps some players believe in a balanced approach to all castles, some emphasize high-point castles, others low-point castles, and so on. Here, I use cluster analysis to examine this hypothesis.
I will be switching from Python to R from this point on, but there's a few things I want to do in Python first: submit strategies from the second round to my database, and generate strategies via the ABM when using strategies from both rounds of the Battle for Riddler Nation as the initial seed.
# Submit round 2 strategies
try:
conn.execute("DROP TABLE round2strats;")
except:
pass
make_table = """CREATE TABLE `round2strats` (
`idx` int(4),
`castle_1` int(8),
`castle_2` int(8),
`castle_3` int(8),
`castle_4` int(8),
`castle_5` int(8),
`castle_6` int(8),
`castle_7` int(8),
`castle_8` int(8),
`castle_9` int(8),
`castle_10` int(8),
PRIMARY KEY (`idx`)
);"""
conn.execute(make_table)
temp_table = riddler_strats.loc[2].copy()
temp_table.columns = pd.Index(["castle_" + str(i) for i in temp_table.columns])
temp_table.to_sql("round2strats", con=conn, if_exists='append')
del temp_table
# Generate combined strategies ABM results
%time rb2 = RiddlerBattle(DataFrame(riddler_strats.values, columns=np.arange(10) + 1))
CPU times: user 5.86 s, sys: 12 ms, total: 5.88 s
Wall time: 6.12 s
%time rb2.run_model(100)
CPU times: user 29min 44s, sys: 1.77 s, total: 29min 46s
Wall time: 30min 17s
warlords2 = rb2.dc.get_agent_vars_dataframe()
warlords2 = DataFrame([w[1]["Doctrine"] for w in warlords2.iterrows()], columns=np.arange(10) + 1,
index=warlords2.index)
# FYI: I'm aware this is bad database design, and I don't care.
try:
conn.execute("DROP TABLE round2simulation;")
except:
pass
make_table = """CREATE TABLE `round2simulation` (
`step` int(4),
`agentid` int(8),
`castle_1` int(8),
`castle_2` int(8),
`castle_3` int(8),
`castle_4` int(8),
`castle_5` int(8),
`castle_6` int(8),
`castle_7` int(8),
`castle_8` int(8),
`castle_9` int(8),
`castle_10` int(8),
PRIMARY KEY (`step`,`agentid`)
);"""
conn.execute(make_table)
temp_table = warlords2.copy()
temp_table.columns = pd.Index(["castle_" + str(i) for i in temp_table.columns])
temp_table.to_sql("round2simulation", con=conn, if_exists='append')
del temp_table
# We're done in Python now; only remaining business is closing the MySQL connection
conn.close()
Now we can start using R.
# Loading packages
pckgs_cran <- c("dplyr",
"ggplot2",
"mclust",
"devtools",
"RMySQL")
for (pckg in pckgs_cran) {
if (!require(pckg, character.only = TRUE)) {
install.packages(pckg)
require(pckg, character.only = TRUE)
}
}
## Loading required package: dplyr
##
## Attaching package: 'dplyr'
## The following objects are masked from 'package:stats':
##
## filter, lag
## The following objects are masked from 'package:base':
##
## intersect, setdiff, setequal, union
## Loading required package: ggplot2
## Loading required package: mclust
## Package 'mclust' version 5.3
## Type 'citation("mclust")' for citing this R package in publications.
## Loading required package: devtools
## Loading required package: RMySQL
## Loading required package: DBI
if (!require("gganimate")) {
devtools::install_github("dgrtwo/gganimate")
library(gganimate)
}
## Loading required package: gganimate
`%s%` <- function(x, y) paste(x, y)
`%s0%` <- function(x, y) paste0(x, y)
Now let's connect to the database so we can work with the data.
db <- src_mysql("riddlerbattles", host = "127.0.0.1", user = "root",
password = pswd)
castle_str <- paste0("castle_", 1:10)
round1_strats <- tbl(db, sql("SELECT" %s% paste(castle_str,
collapse = ", ") %s%
"FROM round1simulation WHERE step = 0"))
round2_strats <- tbl(db, sql("SELECT" %s% paste(castle_str,
collapse = ", ") %s%
"FROM round2strats"))
round1_sim <- tbl(db, sql("SELECT step," %s% paste(castle_str,
collapse = ", ") %s%
"FROM round1simulation"))
round2_sim <- tbl(db, sql("SELECT step," %s% paste(castle_str,
collapse = ", ") %s%
"FROM round2simulation"))
I first will embed the strategies from round 1 into a 2D space, just for the sake of visualization. I do this by finding a distance matrix, then using classical multidimensional scaling to find points in a 2D plane that closely preserve the distance matrix. Here, I feel that Manhattan distance is the best way to describe distances between strategies (it basically translates to how many troops need to be moved for one strategy to become another).
round1_strats_mat % as.data.frame %>% as.matrix
round2_strats_mat % as.data.frame %>% as.matrix
strats_mds %
dist("manhattan") %>% cmdscale
round1_strats_mds <- strats_mds[1:nrow(round1_strats_mat), ]
round2_strats_mds <- strats_mds[-(1:nrow(round1_strats_mat)), ]
round1_strats_plot <- data.frame("x" = round1_strats_mds[, 1],
"y" = round1_strats_mds[, 2])
round2_strats_plot <- data.frame("x" = round2_strats_mds[, 1],
"y" = round2_strats_mds[, 2])
ggplot(round1_strats_plot, aes(x = x, y = y)) +
geom_point() +
theme_bw()
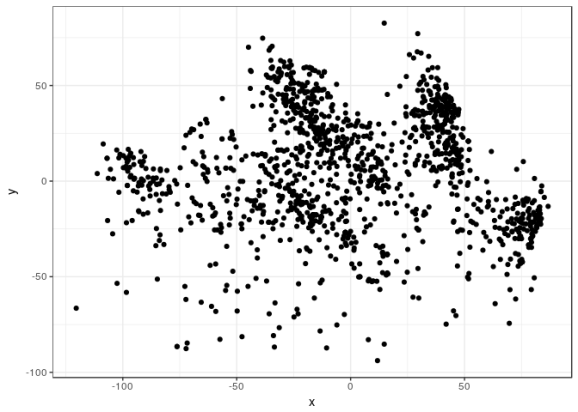
ggplot(round2_strats_plot, aes(x = x, y = y)) + geom_point() + theme_bw()

Clusters definitely exist in the first round. In my opinion, at least five, maybe six clusters exist (I want to consider stragglers a separate cluster). In the second round, I observe more uniformity; my guess is there are between one and four clusters, but most likely one.
I want to know how performance in the Battle is distributed. For this, I'll need an adjudicator, but I can write one for R similarly to how I wrote one in Python with NumPy.
# Interesting: this is barely slower than the Python original
battle_strat_df <- function(df1, df2) {
# Adjudicate all battles to see who wins
#
# args:
# df1: matrix; A matrix of warlords' strategies
# df2: matrix; A matrix of warlords' strategies
# return:
# matrix; Contains columns for Win, Tie, and Lose, the performance
# of the warlords of df1 against those of df2
score_mat <- matrix(rep(1:10, times = nrow(df2)), nrow = nrow(df2),
byrow = TRUE)
res <- sapply(1:nrow(df1), function(i) {
vec <- df1[i, ]
margin <- matrix(rep(vec, times = nrow(df2)), nrow = nrow(df2)) - df2
df1_castles 0) * score_mat
df2_castles <- (margin < 0) * score_mat
tie_castles <- (margin == 0) * score_mat
tie_scores <- rowSums(tie_castles) / 2
df1_scores <- rowSums(df1_castles) + tie_scores
df2_scores df2_scores),
"Tie" = sum(df1_scores == df2_scores),
"Losses" = sum(df1_scores < df2_scores)))
})
return(t(res))
}
round1_res <- battle_strat_df(round1_strats_mat, round1_strats_mat)
round1_strats_plot$win <- (round1_res[, "Win"] / nrow(round1_strats_mat))
round2_res <- battle_strat_df(round2_strats_mat, round2_strats_mat)
round2_strats_plot$win <- (round2_res[, "Win"] / nrow(round2_strats_mat))
ggplot(round1_strats_plot, aes(x = x, y = y, color=win)) +
geom_point() +
scale_color_gradient(low = "dark blue", high = "orange") +
theme_bw()

ggplot(round2_strats_plot, aes(x = x, y = y, color=win)) + geom_point() + scale_color_gradient(low = "dark blue", high = "orange") + theme_bw()

Judging from these charts, strategies near the periphery don't do very well, while those near the center tend to do better. A peripheral strategy probably resembles (100, 0, 0, 0, 0, 0, 0, 0, 0, 0), but the winning strategies look, in some sense, "balanced". With that in mind, these pictures are not too shocking. Looking at the first chart for the first round one may guess that some clusters consist of well performing strategies, while other clusters consist of more poor performers.
Let's see if we can use this embedding and mclust to determine what the clusters are. mclust is an R package for model-based clustering; that is, it applies the EM-algorithm to find a clustering scheme that works well for data that was drawn from Normally distributed clusters. If you're familiar with k-means clustering, model-based clustering via the EM-algorithm and a Normal model is a much more sophisticated version of the same thing.
mclust's principal function, Mclust(), takes automated steps to find a good clustering scheme. I simply run it out of the box to find clusters for both data sets.
clust1 <- Mclust(round1_strats_mds, G=1:6) summary(clust1) ## ---------------------------------------------------- ## Gaussian finite mixture model fitted by EM algorithm ## ---------------------------------------------------- ## ## Mclust VEV (ellipsoidal, equal shape) model with 5 components: ## ## log.likelihood n df BIC ICL ## -13023.54 1349 25 -26227.25 -26471.11 ## ## Clustering table: ## 1 2 3 4 5 ## 75 575 123 310 266 round1_strats_plot$clust <- as.factor(clust1$classification) ggplot(round1_strats_plot, aes(x = x, y = y, color=clust)) + geom_point() + scale_color_brewer(palette = "Dark2") + theme_bw()

clust2 <- Mclust(round2_strats_mds, G=1:4) summary(clust2) ## ---------------------------------------------------- ## Gaussian finite mixture model fitted by EM algorithm ## ---------------------------------------------------- ## ## Mclust VVI (diagonal, varying volume and shape) model with 3 components: ## ## log.likelihood n df BIC ICL ## -8741.765 902 14 -17578.79 -17678.37 ## ## Clustering table: ## 1 2 3 ## 735 25 142 round2_strats_plot$clust <- as.factor(clust2$classification) ggplot(round2_strats_plot, aes(x = x, y = y, color=clust)) + geom_point() + scale_color_brewer(palette = "Dark2") + theme_bw()
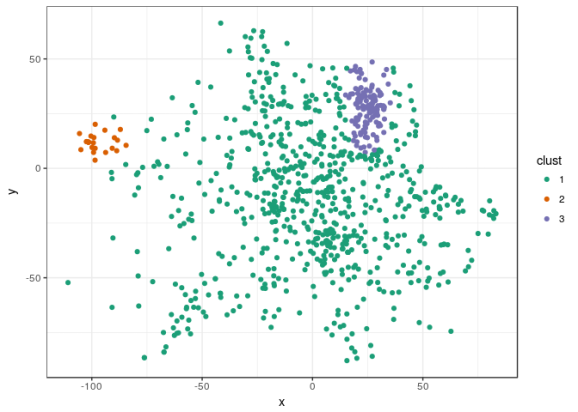
I would say reasonable clustering were found both times, and they largely affirm what I believed; there's five good clusters in the first round, but by the second round players started to converge to variations on one strategy (it may have found three clusters, but they're not very convincing).
Let's characterize the clusters even more.
clust_strats1 <- t(sapply(unique(clust1$classification),
function(c) colMeans(round1_strats_mat[which(
clust1$classification == c), ])))
clust_strats1 %>% round(digits = 0)
## castle_1 castle_2 castle_3 castle_4 castle_5 castle_6 castle_7
## [1,] 3 3 4 6 7 10 12
## [2,] 4 7 8 10 9 10 6
## [3,] 7 8 9 13 17 20 24
## [4,] 1 2 2 5 7 12 17
## [5,] 2 4 4 8 13 18 23
## castle_8 castle_9 castle_10
## [1,] 17 19 19
## [2,] 3 12 31
## [3,] 1 1 1
## [4,] 25 27 1
## [5,] 27 1 1
clust_strats1 %>% heatmap(Colv=NA)

clust_wins1 <- sapply(unique(clust1$classification),
function(c) {
res <- battle_strat_df(round1_strats_mat[which(
clust1$classification == c
), ], round1_strats_mat)
return(mean(res[, "Win"] / nrow(round1_strats_mat)))
})
names(clust_wins1) <- 1:5
clust_wins1
## 1 2 3 4 5
## 0.3497831 0.3156116 0.3306334 0.3121045 0.3097644
clust_strats2 <- t(sapply(unique(clust2$classification),
function(c) colMeans(round2_strats_mat[which(
clust2$classification == c), ])))
clust_strats2 %>% round(digits = 0)
## castle_1 castle_2 castle_3 castle_4 castle_5 castle_6 castle_7
## [1,] 3 4 6 8 10 13 13
## [2,] 7 1 0 0 0 0 0
## [3,] 2 4 5 7 11 10 24
## castle_8 castle_9 castle_10
## [1,] 14 15 13
## [2,] 31 30 29
## [3,] 30 4 4
clust_strats2 %>% heatmap(Colv=NA)

clust_wins2 <- sapply(unique(clust2$classification),
function(c) {
res <- battle_strat_df(round2_strats_mat[which(
clust2$classification == c
), ], round2_strats_mat)
return(mean(res[, "Win"] / nrow(round2_strats_mat)))
})
names(clust_wins2) <- 1:3
clust_wins2
## 1 2 3
## 0.3464018 0.1466962 0.3247166
In the first round, we can see that there were five doctrines for troop allocation. Doctrines 1 and 2 bet heavy on high-value castles, and the other three were varying degrees of betting on low-value castles, with the most successful of the three groups betting almost exclusively on low-value castles, ignoring those with a value greater than 7. The other two were less successful the more they bet on high-value castles.
In the second round, people tended to spread out their troop allocations more. Most gravitated towards an even distribution of troops among castles with values of at least 6. The least successful group, and also the smallest group, continued to bet heavy on high-value castles, and a subset bet slightly more heavily on lower-value castles.
Strategy Evolution
Finally, I want to look at how strategies developed during the simulation evolved.
In spirit, I repeat the multidimensional scaling, clustering, and plotting I did above, but clusters are found on data that extends across time (I hope this shows, say, a speciation process, or perhaps homogenization), and the plot is animated.
This is all done for the first simulation, using strategies submitted in only the first round, below. Unfortunately, the classical multidimensional scaling method and model-based clustering methods that I implemented before won't work here; they're too computationally taxing, and simply fail and crash R. Since the matrix off strategies is large, I'm not surprised, but I am disappointed. I had to resort to PCA and using the first two principal components, and using k-means for clustering instead of model-based clustering.
round1_sims_mat <- round1_sim %>% as.data.frame %>% as.matrix
round1_sims_mds <- cbind(princomp(round1_sims_mat[, 2:11],
scores = TRUE)$scores[, 1:2],
round1_sims_mat[, "step"])
colnames(round1_sims_mds) <- c("x", "y", "step")
sims_clust1 <- kmeans(round1_sims_mds[,1:2], centers = 10)$cluster
round1_sims_plot <- data.frame("x" = round1_sims_mds[,"x"],
"y" = round1_sims_mds[,"y"],
"step" = round1_sims_mds[,"step"],
"clust" = as.factor(sims_clust1))
p <- ggplot(round1_sims_plot, aes(x = x, y = y, color = clust, frame = step)) +
geom_point() +
theme_bw()
gganimate(p, "out.gif", interval = .2)
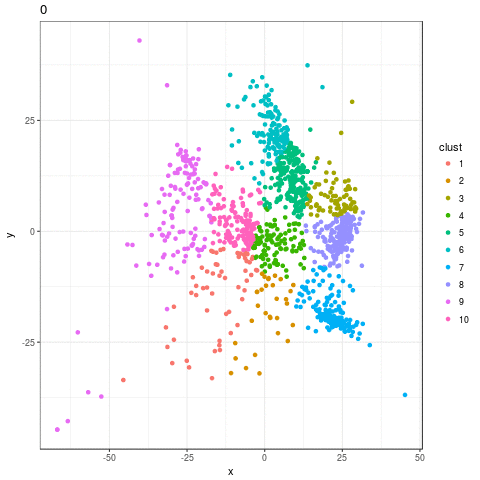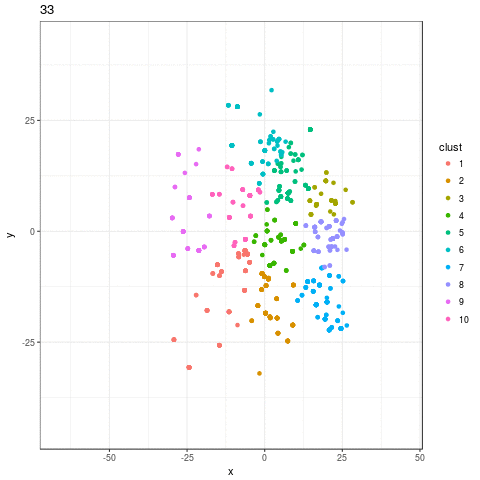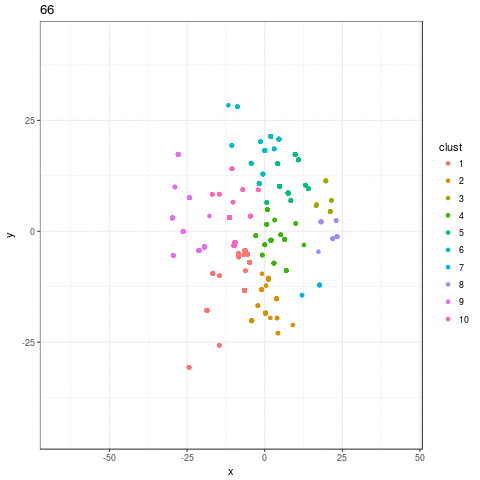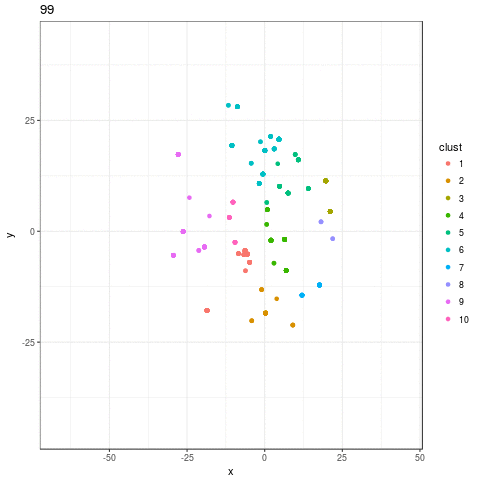
I was disappointed by the result. I expected to see exploration of the feature space, species being born and going extinct, but all I see is mass population die-off as the algorithm converges on a small handful of survivors. Flimsy strategy choices are weened out, and eventually more and more weak choices die out, but there's no reason to think that the algorithm is allowing individuals with good characteristics (that is, good choice of doctrine) not necessarily included in the initial set of strategies to be born and challenge incumbents.
If my strategy is not performing well, this is likely the explanation: not enough exploration of the possible space of strategies. This suggests allow for more radical evolution in the ABM as opposed to what is currently being employed.
Here is the simulation on a larger starting strategy set, including the strategies from both round 1 and round 2. The result is basically the same.
round2_sims_mat <- round2_sim %>% as.data.frame %>% as.matrix
round2_sims_mds <- cbind(princomp(round2_sims_mat[, 2:11],
scores = TRUE)$scores[, 1:2],
round2_sims_mat[, "step"])
colnames(round2_sims_mds) <- c("x", "y", "step")
sims_clust2 <- kmeans(round2_sims_mds[,1:2], centers = 10)$cluster
round2_sims_plot <- data.frame("x" = round2_sims_mds[,"x"],
"y" = round2_sims_mds[,"y"],
"step" = round2_sims_mds[,"step"],
"clust" = as.factor(sims_clust2))
p <- ggplot(round2_sims_plot, aes(x = x, y = y, color = clust, frame = step)) +
geom_point() +
theme_bw()
gganimate(p, "out2.gif", interval = .2)

Conclusion
There's a lot to learn from these data sets. I want to see what words appear in players' description of their strategies' motivation, allowing me to discover thought patterns in strategy clusters. I also want to see if a neural network could be used to learn good strategies.
That said, the ABM method appears to need tweaking. The winning strategy's author said he was using genetics-based algorithms to find his solution, a commonly recurring theme. I thought I was using a genetic algorithm, but it seems that although the weak die off and the strong reproduce, there are not enough mutations in my model to allow finding a good strategy. Maybe this could be fixed by parameter tuning. I don't know. We will need to see.
That said, this has been a fun project, and I have learned a lot in the process. Perhaps next time I will reign supreme over Riddler Nation.
- As mentioned in my first article, I was not able to replicate Mr. Roeder’s records, and I did not find the same winning strategies as he did. I do not know where the source of the error is, but I looked over my code a lot and cannot find errors in it. ↩
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
