R Tutorial: Visualizing Multivariate Relationships in Large Datasets
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
R Tutorial: Visualizing multivariate relationships in Large Datasets
A tutorial by D.M. Wiig
In two previous blog posts I discussed some techniques for visualizing relationships involving two or three variables and a large number of cases. In this tutorial I will extend that discussion to show some techniques that can be used on large datasets and complex multivariate relationships involving three or more variables.
In this tutorial I will use the R package nmle which contains the dataset MathAchieve. Use the code below to install the package and load it into the R environment:
####################################################
#code for visual large dataset MathAchieve
#first show 3d scatterplot; then show tableplot variations
####################################################
install.packages(“nmle”) #install nmle package
library(nlme) #load the package into the R environment
####################################################
Once the package is installed take a look at the structure of the data set by using:
####################################################
attach(MathAchieve) #take a look at the structure of the dataset
str(MathAchieve)
####################################################
Classes ‘nfnGroupedData’, ‘nfGroupedData’, ‘groupedData’ and ‘data.frame’: 7185 obs. of 6 variables:
$ School : Ord.factor w/ 160 levels “8367”<“8854″<..: 59 59 59 59 59 59 59 59 59 59 …
$ Minority: Factor w/ 2 levels “No”,”Yes”: 1 1 1 1 1 1 1 1 1 1 …
$ Sex : Factor w/ 2 levels “Male”,”Female”: 2 2 1 1 1 1 2 1 2 1 …
$ SES : num -1.528 -0.588 -0.528 -0.668 -0.158 …
$ MathAch : num 5.88 19.71 20.35 8.78 17.9 …
$ MEANSES : num -0.428 -0.428 -0.428 -0.428 -0.428 -0.428 -0.428 -0.428 -0.428 -0.428 …
– attr(*, “formula”)=Class ‘formula’ language MathAch ~ SES | School
.. ..- attr(*, “.Environment”)=
– attr(*, “labels”)=List of 2
..$ y: chr “Mathematics Achievement score”
..$ x: chr “Socio-economic score”
– attr(*, “FUN”)=function (x)
..- attr(*, “source”)= chr “function (x) max(x, na.rm = TRUE)”
– attr(*, “order.groups”)= logi TRUE
>
As can be seen from the output shown above the MathAchieve dataset consists of 7185 observations and six variables. Three of these variables are numeric and three are factors. This presents some difficulties when visualizing the data. With over 7000 cases a two-dimensional scatterplot showing bivariate correlations among the three numeric variables is of limited utility.
We can use a 3D scatterplot and a linear regression model to more clearly visualize and examine relationships among the three numeric variables. The variable SES is a vector measuring socio-economic status, MathAch is a numeric vector measuring mathematics achievment scores, and MEANSES is a vector measuring the mean SES for the school attended by each student in the sample.
We can look at the correlation matrix of these 3 variables to get a sense of the relationships among the variables:
> ####################################################
> #do a correlation matrix with the 3 numeric vars;
> ###################################################
> data(“MathAchieve”)
> cor(as.matrix(MathAchieve[c(4,5,6)]), method=”pearson”)
SES MathAch MEANSES
SES 1.0000000 0.3607556 0.5306221
MathAch 0.3607556 1.0000000 0.3437221
MEANSES 0.5306221 0.3437221 1.0000000
>
In using the cor() function as seen above we can determine the variables used by specifying the column that each numeric variable is in as shown in the output from the str() function. The 3 numeric variables, for example, are in columns 4, 5, and 6 of the matrix.
As discussed in previous tutorials we can visualize the relationship among these three variable by using a 3D scatterplot. Use the code as seen below:
####################################################
#install.packages(“nlme”)
install.packages(“scatterplot3d”)
library(scatterplot3d)
library(nlme) #load nmle package
attach(MathAchieve) #MathAchive dataset is in environment
scatterplot3d(SES, MEANSES, MathAch, main=”Basic 3D Scatterplot”) #do the plot with default options
####################################################
The resulting plot is:
Even though the scatter plot lacks detail due to the large sample size it is still possible to see the moderate correlations shown in the correlation matrix by noting the shape and direction of the data points . A regression plane can be calculated and added to the plot using the following code:
scatterplot3d(SES, MEANSES, MathAch, main=”Basic 3D Scatterplot”) #do the plot with default options
####################################################
##use a linear regression model to plot a regression plane
#y=MathAchieve, SES, MEANSES are predictor variables
####################################################
model1=lm(MathAch ~ SES + MEANSES) ## generate a regression
#take a look at the regression output
summary(model1)
#run scatterplot again putting results in model
model <- scatterplot3d(SES, MEANSES, MathAch, main=”Basic 3D Scatterplot”) #do the plot with default options
#link the scatterplot and linear model using the plane3d function
model$plane3d(model1) ## link the 3d scatterplot in ‘model’ to the ‘plane3d’ option with ‘model1’ regression information
####################################################
The resulting output is seen below:
Call:
lm(formula = MathAch ~ SES + MEANSES)
Residuals:
Min 1Q Median 3Q Max
-20.4242 -4.6365 0.1403 4.8534 17.0496
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 12.72590 0.07429 171.31 <2e-16 ***
SES 2.19115 0.11244 19.49 <2e-16 ***
MEANSES 3.52571 0.21190 16.64 <2e-16 ***
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 6.296 on 7182 degrees of freedom
Multiple R-squared: 0.1624, Adjusted R-squared: 0.1622
F-statistic: 696.4 on 2 and 7182 DF, p-value: < 2.2e-16
and the plot with the plane is:
While the above analysis gives us useful information, it is limited by the mixture of numeric values and factors. A more detailed visual analysis that will allow the display and comparison of all six of the variables is possible by using the functions available in the R package Tableplots. This package was created to aid in the visualization and inspection of large datasets with multiple variables.
The MathAchieve contains a total of six variables and 7185 cases. The Tableplots package can be used with datasets larger than 10,000 observations and up to 12 or so variables. It can be used visualize relationships among variables using the same measurement scale or mixed measurement types.
To look at a comparisons of each data type and then view all 6 together begin with the following:
####################################################
attach(MathAchieve) #attach the dataset
#set up 3 data frames with numeric, factors, and mixed
####################################################
mathmix <- data.frame(SES,MathAch,MEANSES,School=factor(School),Minority=factor(Minority),Sex=factor(Sex)) #all 6 vars
mathfact <- data.frame(School=factor(School),Minority=factor(Minority),Sex=factor(Sex)) #3 factor vars
mathnum <- data.frame(SES,MathAch,MEANSES) #3 numeric vars
####################################################
To view a comparison of the 3 numeric variables use:
####################################################
require(tabplot) #load tabplot package
tableplot(mathnum) #generate a table plot with numeric vars only
####################################################
resulting in the following output:
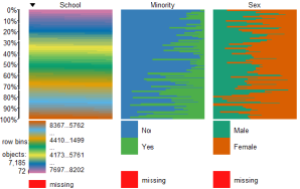
To view only the 3 factor variables use:
####################################################
require(tabplot) #load tabplot package
tableplot(mathfact) #generate a table plot with factors only
####################################################
Resulting in:
To view and compare table plots of all six variables use:
####################################################
require(tabplot) #load tabplot package
tableplot(mathmix) #generate a table plot with all six variables
####################################################
Resulting in:
Using tableplots is useful in visualizing relationships among a set of variabes. The fact that comparisons can be made using mixed levels of measurement and very large sample sizes provides a tool that the researcher can use for initial exploratory data analysis.
The above visual table comparisons agree with the moderate correlation among the three numeric variables found in the correlation and regression models discussed above. It is also possible to add some additional interpretation by viewing and comparing the mix of both factor and numeric variables.
In this tutorial I have provided a very basic introduction to the use of table plots in visualizing data. Interested readers can find an abundance of information about Tableplot options and interpretations in the CRAN documentation.
In my next tutorial I will continue a discussion of methods to visualize large and complex datasets by looking at some techniques that allow exploration of very large datasets and up to 12 variables or more.
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.