Working with spatial data in R I find myself quite often in the need to quickly visually check whether a certain analysis has produced reasonable results. There are two ways I usually do this. Either I:

1. (sp)plot the data in R and then toggle back and forth between the static plots (I use RStudio) or
2. save the data to the disk and then open in QGIS or similar to interactively examine the results.

Both these approaches are semi-optimal. Where option 1. is fine for a quick glance at a coarse patterns, it lacks the possibility to have a closer look into the results via zooming and paning. While option 2. provides the interactivity, the detour via the hard disk is annoying (at best), especially when fine-tuning and checking regularly.

I attended this years useR2015! conference in Aalborg (which was marvelous!) and attended the session on interactive graphics in R where Joe Cheng from RStudio presented the leaflet package. Leaflet is great but its rather geared towards manually setting up maps. What a GIS-like functionality would need is some default behaviour for different objects from the spatial universe.

This got me thinking and sparked my enthusiasm to write some wrapper functions for leaflet to provide at least very basic GIS-like interactive graphing capabilities that are directly accessible within RStudio (or the web browser, if you're not using RStudio). So I sat down and wrote a function called mapView().

Unfortunately, it is not possible to present interactive leaflet content here at wordpress.

Therefore, the full article is published at web presentations space at github.

Here's a little sneak preview though.

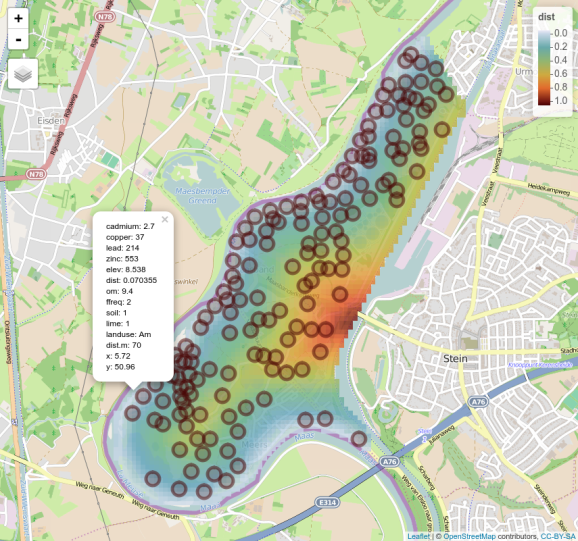
Enjoy reading!

Tim