Basketball Data Part II – Length of Career by Position
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
In the previous post, I showed how easy it is to use R to scrape XML tables from websites (I used the XML package to scrape some basic basketball data). In this post, I’ll explore the idea that NBA career length might vary by position. Before reviewing this data, I assumed that centers (and big men in general) would have the shortest NBA careers. My theory was that these guys were just too big to stay healthy long enough to string together a career – they’re just too big. Let’s see what the data says:
It seems like the median career length is 2 years for centers, guards, and forwards. We can see that centers and guards tend to have longer careers than forwards in general. If we look and C-F and G-F, we can see that these players average significantly longer careers than single position players. I don’t know a lot about basketball, so its difficult for me to speculate why these players have longer careers. Maybe they’re so athletic that they can easily play either position and more athletic players tend to have longer careers? Maybe these players have been in the league so long that they get moved around and thus earn the “C-F” or “G-F” designation? Any theories from people who know more about basketball?
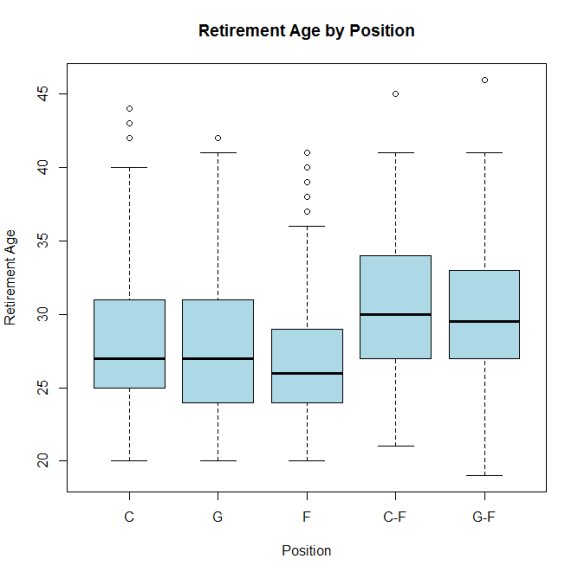
I also looked briefly at retirement age:
We can see a similar trend here with centers and guards retiring later than forwards (and C-F/G-F players retiring later than all single position players). More than 75% of forwards retire from the NBA before their 30′s. I’m 29 now. Good thing I’m not a forward…
Here is the code:
###### Settings
library(XML)
setwd("C:/Blog/Basketball")
###### URLs
url<-paste0("http://www.basketball-reference.com/players/",letters,"/")
len<-length(url)
###### Reading data
tbl<-readHTMLTable(url[1])[[1]]
for (i in 2:len)
{tbl<-rbind(tbl,readHTMLTable(url[i])[[1]])}
###### Formatting data
colnames(tbl)<-c("Name","StartYear","EndYear","Position","Height","Weight","BirthDate","College")
tbl$BirthDate<-as.Date(tbl$BirthDate,format="%B %d, %Y")
tbl$StartYear<-as.numeric(as.character(tbl$StartYear))
tbl$EndYear<-as.numeric(as.character(tbl$EndYear))
tbl$Position[tbl$Position=="F-C"]<-"C-F"
tbl$Position[tbl$Position=="F-G"]<-"G-F"
tbl$Position<-factor(tbl$Position,levels=c("C","G","F","C-F","G-F"))
###### Career Length
tbl$LEN<-tbl$EndYear-tbl$StartYear
table(tbl$Position)
boxplot(tbl$LEN~tbl$Position,col="light blue",ylab="Years",xlab="Position",
main="Length of Career by Position")
###### Age at Retirement
tbl$RetireAge<-tbl$EndYear-as.numeric(substr(tbl$BirthDate,0,4))
boxplot(tbl$RetireAge~tbl$Position,col="light blue",ylab="Retirement Age",xlab="Position",
main="Retirement Age by Position")
###### Removing Currently Active Players
retired<-tbl[tbl$EndYear<2014,]
boxplot(tbl$LEN~tbl$Position,col="light blue",ylab="Years",xlab="Position",
main="Length of Career by Position")
boxplot(tbl$RetireAge~tbl$Position,col="light blue",ylab="Retirement Age",xlab="Position",
main="Retirement Age by Position")
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.