We are happy to introduce Reot, an R package designed for empirical orthogonal teleconnection (EOT) analysis of gridded geo-scientific space-time data based on the method by van den Dool et al. (2000). EOT denotes a regression-based approach to decompose spatio-temporal fields into a set of independent orthogonal patterns. In contrast to the classical approach of Empirical Orthogonal Functions (EOF), which are orthogonal in space and time, EOT analysis produces patterns that are orthogonal in either space or time (the current implementation of Reot provides the latter).

To identify these patterns, the time series of each pixel pp of the predictor domain is regressed against the time series of all pixels pr in the response domain (in case of a single field pr = pp – 1). The pixel with the highest sum of its coefficients of determination is defined as the ’base point’ of the first/leading mode. The time series of this point is the first/leading EOT. The next EOT is calculated on the residuals of the previous step, thus ensuring orthogonality of the modes. This procedure is repeated until a user-specified number of EOTs is identified.

Given that the amount of regressions to be calculated can be extremely large, we implemented the core regression functions of Reot in C++ (via Rcpp) to ensure acceptable computation times. All input and output is based on Raster* classes to ensure seamless integration with existing analysis tools and work-flows. Reot is available from CRAN. The development version is hosted on GitHub.

Examples

Example 1: Winter mean 700 mb height over the Northern Hemisphere

As a first example, we replicate one of the examples from van den Dool et al. (2000) (Example 3.d. – Figure 6). A spatio-temporal field of 700 mb geopotential heights of NCEP/NCAR Reanalysis grids Kalnay et al. (1996) is decomposed into its four leading modes exhibiting the prominent patterns of North Atlantic Oscillation (NAO) and Pacific-North American Pattern (PNA) as modes 1 and 2, respectively. The climatologically inclined reader is referred to the respective Section in van den Dool et al. (2000) for a more detailed description of the atmospheric dynamics and processes associated with the identified patterns. Here, we merely want to highlight, that the Reot implementation of the algorithm produces similar results to the original implementation by van den Dool et al. (2000).

library("rworldmap")
library("rgdal")
library("rgeos")
library("latticeExtra")
library("gridExtra")
library("Reot")

### load the necessary data
data("vdendool")
data("coastsCoarse")

### calculate the first four EOT modes
modes <- eot(pred = vdendool, resp = NULL, n = 4, 
             reduce.both = FALSE, standardised = FALSE, 
             print.console = TRUE)

## 
## Calculating linear model ... 
## Locating 1. EOT ...
## Location: -35 77.67 
## Cum. expl. variance (%): 21.53 
## 
## Calculating linear model ... 
## Locating 2. EOT ...
## Location: -165 43.15 
## Cum. expl. variance (%): 38.17 
## 
## Calculating linear model ... 
## Locating 3. EOT ...
## Location: 85 67.81 
## Cum. expl. variance (%): 46.08 
## 
## Calculating linear model ... 
## Locating 4. EOT ...
## Location: -25 53.01 
## Cum. expl. variance (%): 53.07


### set appropriate projection
ster <- CRS("+proj=stere +lat_0=90 +lon_0=-45")

xmin <- -180
xmax <- 180
ymin <- 20
ymax <- 90     # Coordinates for bounding box
bb <- cbind(x = c(xmin, xmin, xmax, xmax, xmin), 
            y = c(ymin, ymax, ymax, ymin, ymin))
SP <- SpatialPolygons(list(Polygons(list(Polygon(bb)), 
                                    "1")), 
                      proj4string = CRS(proj4string(coastsCoarse)))

gI <- gIntersects(coastsCoarse, SP, byid = TRUE) 
out <- vector(mode = "list", length = length(which(gI))) 
ii <- 1

for (i in seq(along = gI)) if (gI[i]) {
  out[[ii]] <- gIntersection(coastsCoarse[i, ], SP)
  row.names(out[[ii]]) <- row.names(coastsCoarse)[i]
  ii <- ii + 1
  }

nhem.coasts <- do.call("rbind", out)
nhem.coasts.ster <- spTransform(nhem.coasts, ster) 

lout <- list("sp.lines", nhem.coasts.ster, 
             col = "grey30", grid = TRUE)

### define colors
clrs <- colorRampPalette(rev(brewer.pal(9, "RdBu")))

### re-project modes
mode <- lapply(seq(modes), function(i) {
  projectRaster(modes[[i]]$r.predictor, crs = ster)
  })

### create title for each image
titles <- lapply(seq(mode), function(i) {
  paste("Mode ", i, " : ", "EV = ", 
        round(if (i > 1) {
          modes[[i]]$exp.var * 100 - 
            modes[[i - 1]]$exp.var * 100
          } else {
            modes[[i]]$exp.var * 100
            }, 1), " : ", "BP = ", 
        as.integer(modes[[i]]$loc.eot[, 1]), 
        ", ", as.integer(modes[[i]]$loc.eot[, 2]), 
        sep = "")
  })

### create plots
p <- lapply(seq(mode), function(i) {
  spplot(mode[[i]], sp.layout = lout, 
         main = list(titles[[i]], cex = 0.7),
         col.regions = clrs(1000), at = seq(-1, 1, 0.2),
         par.settings = list(axis.line = list(col = 0)),
         colorkey = list(height = 0.75, width = 1))
  })

### arrange and plot
f <- function(...) grid.arrange(..., heights = 1, ncol = 2)
do.call(f, p)

Even though the location of the identified base points (BP) is somewhat offset, and hence the explained variance (EV) figures differ slightly compared to van den Dool (2000), it is obvious that the isolated patterns are very similar and represent the same signals. We can only speculate as to why the base point locations differ slightly, but potential reasons may include different version numbers of the reanalysis data, rounding discrepancies between the utilised programming languages (especially when summing up the coefficients of determination) and slight differences in geographic projections.

Example 2: Identifying tropical Pacific SST drivers for Australian precipitation

The processes of precipitation development are complex and not yet understood completely. The physical state of the atmosphere, which determines whether rain occurs or not at any point in space and time, is the result of a multitude of constantly changing factors. Influences range from local to hemispheric boundary conditions in all 4 dimensions (incl. time).

Some areas of the global oceans exhibit low-frequency anomaly signals which can influence precipitation variability world-wide. The most prominent example of a coupled ocean-atmosphere tropical SST variability is ENSO. ENSO has received much attention in the scientific literature since the major 1982 – 83 El Nino. Here we investigate, whether EOT analysis can be used to identify the ENSO signal as a driver for low-frequency Australian precipitation variability over the period 1982 to 2010. The data sets needed for this analysis are included in Reot. In order to reveal low-frequency signals such as ENSO, we need to prepare the raw data fields so that high-frequency variation is eliminated. We achieve this by creating seasonal anomalies using deseson() and by denoise()-ing the data to filter out some of the noise that is present in any spatio-temporal data field.

The first 3 leading modes of SSTs most influential for Australian rainfall variability can be calculated with:

data("australiaGPCP")
data("pacificSST")

sst.pred <- deseason(pacificSST, cycle.window = 12)
gpcp.resp <- deseason(australiaGPCP, cycle.window = 12)

sst.pred.dns <- denoise(sst.pred, expl.var = 0.9)

## 
## Using the first 19 components (of 348) to reconstruct series...
##  these account for 0.9 of variance in orig. series

gpcp.resp.dns <- denoise(gpcp.resp, expl.var = 0.9)

## 
## Using the first 37 components (of 348) to reconstruct series...
##  these account for 0.9 of variance in orig. series


modes <- eot(pred = sst.pred.dns, resp = gpcp.resp.dns, 
             n = 3, standardised = FALSE, 
             reduce.both = FALSE, print.console = FALSE)

As we can see, especially the principal components filter from denoise() is an important step, as we need only 19 (37) of the original 348 components for the SST (GPCP) data to explain 90 % of the respective inherent field variance.
To get a visual impression, the results for the first leading mode can be plotted using the standard Reot plotting routine plotEot():

plotEot(modes, eot = 1, 
        show.eot.loc = TRUE, 
        arrange = "long")

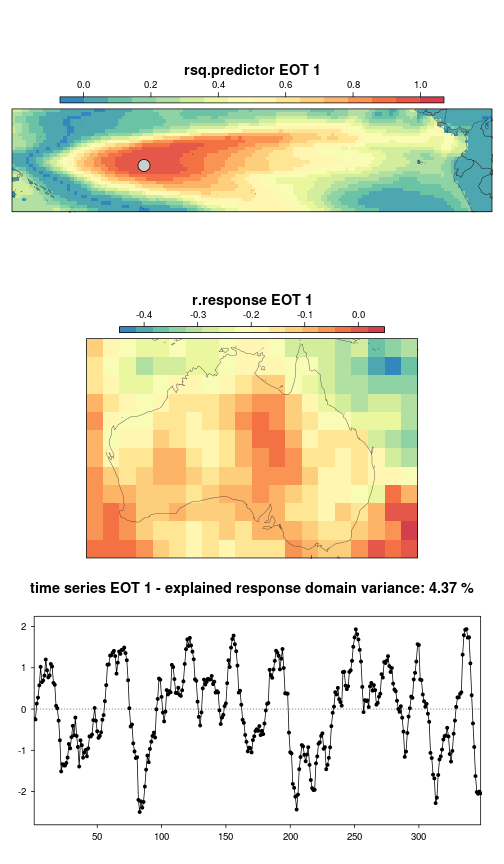
We see that we are indeed able to isolate the ENSO signal as the most important SST driver in the tropical Pacific (EOT 1) for Australian precipitation. This signal is able to explain just above 4 % of the original variation found in rainfall over the analysed period. This may not seem much, but we need to keep in mind that precipitation is influenced by many factors, with local conditions playing a major role. Spatially, mainly the north-eastern part of the response domain is being explained with some locations showing negative correlations of up to 0.4. With regard to mainland Australia, it becomes obvious that the identified ENSO signal is not able to explain any rainfall variation in the inner-continental parts of the land mass. It is mainly the coastal areas that are influenced by the ENSO phenomenon. Note, that our analysis did not take into account any time-lags between the SST anomalies and precipitation. Even though in this particular example lagging does not increase the explanatory power of the SST signal (not shown), it can be expected that in many cases the influence will not manifest instantaneously and that a certain lag time will explain a higher portion of the rainfall variance.

Final remarks

We have just submitted a manuscript to the Journal of Statistical Software that describes Reot in much more detail. I will announce more on Reot once the final version of the paper is out, including another example of spatially downscaling NDVI observations from 8 km resolution to 250 m resolution.

For now, I would like to encourage people to try Reot in many different ways and applications and share their feedback with us. Feature requests and/or bug reports should be made on GitHub.

References

Kalnay E, Kanamitsu M, Kistler R, Collins W, Deaven D, Gandin L, Iredell M, Saha S, White G, Woollen J, Zhu Y, Chelliah M, Ebisuzaki W, Higgins W, Janowiak J, Mo K, Ropelewski C, Wang J, Leetmaa A, Reynolds R, Jenne R, Joseph D (1996). “The NCEP/NCAR 40-year reanalysis project.” Bulletin of the American Meteorological Society, 77(3), 437 – 471.

van den Dool HM, Saha S, Johansson A (2000). “Empirical orthogonal teleconnections.” Journal of Climate, 13(8), 1421 – 1435. URL http://journals.ametsoc.org/doi/abs/10.1175/1520-0442(2000)013%3C1421%3AEOT%3E2.0.CO%3B2.