A very special package that I am rather excited about arrived in the mail recently. The package contained a set of 6-sided dice. These dice, however, don’t have the standard numbers one to six on their faces. Instead, they have assorted numbers between zero and nine. Here’s the exact configuration:

red<-c(4,4,4,4,4,9)
blue<-c(2,2,2,7,7,7)
olive<-c(0,5,5,5,5,5)
yellow<-c(3,3,3,3,8,8)
magenta<-c(1,1,6,6,6,6)

Aside from maybe making for a more interesting version of snakes and ladders, why the heck am I so excited about these wacky dice? To find out what makes them so interesting, lets start by just rolling one against another and seeing which one rolls the higher number. Simple enough. Lets roll Red against Blue. Until you get your own set, you can roll in silico.

That was fun. We can do it over and over again and we’ll find that Red beats Blue more often than not. So it seems like Red is a pretty good bet. Now lets try rolling Olive against Red. I’ll wait.

Hey, look at that, the mighty Red has fallen. Olive tends to roll a higher number than Red more often than it doesn’t. So far, we have discovered this relationship:

Olive > Red > Blue

All hail the dominant Olive! Out of these three dice, if we want the best chance of winning, we should always pick Olive right? No dice, as they say. When we roll Olive against Blue, we find that Blue wins more often!

For any one of these three dice, there is another that will roll a higher number more often than not.

Olive > Red > Blue > Olive > Red > Blue > Olive > Red > Blue..

This forms a chain of dominance relationships that is a closed cycle. This property is called intransivity, and you can use it to win riches beyond your wildest dreams, er, well, at least to impress your friends.

Neat, right? But there’s more! We can do the same trick with Yellow, Magenta, and Red (Red > Magenta > Yellow > Red > …). With all five dice, there is a chain for which the order is given by that length of the word for each colour.

Red > Blue > Olive > Yellow > Magenta > …

Awesome. But that’s not it, either! You may have noticed from our three way comparisons that there is another five way chain. This time, the chain order is given by the alphabetical order of the words for each of the colours.

Blue > Magenta > Olive > Red > Yellow > …

What are the odds?

So far I’ve just asked you to take my word for it that the dominance relationships are as I described. Working out the odds of winning for any given pairing of dice as actually quite straightforward. Start by looking at the number on each side of the first die, one at a time. Count how many sides on the opposing die are less than the current number and divide by six. Since each side on the first die has a 1/6 chance of appearing, divide by 6 again. Sum these values for all six sides and you will have the probability that the first die will roll a higher number than the second.

For example, P(Red > Blue) = 5/6 x 1/2 + 1/6, which is 7/12.

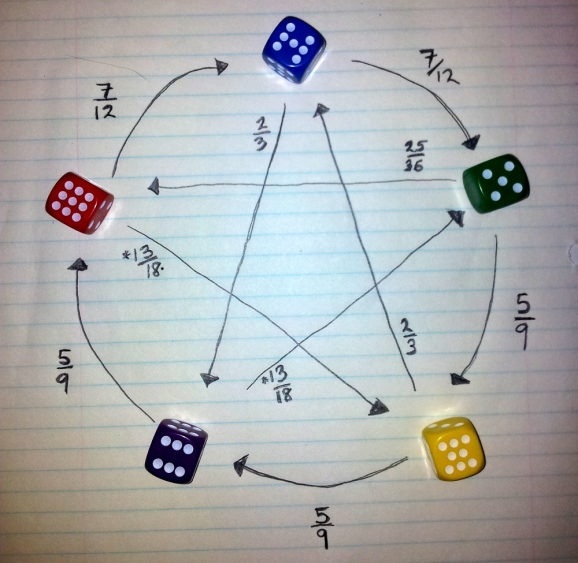
Here I’ve worked out all of the pairwise odds:

So, you can always win in this game as long as you get to be second to choose a colour. The odds are strongest in your favour when your opponent either chooses Magenta or Red, and you choose Olive or Yellow, respectively. Isn’t probability wonderful!

And if you still want more, it turns out that if you roll the Grime dice in pairs, the order of the word length chain reverses!