Fun with random effects in loss reserving
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
For some time now, I’ve advocated for the view that non-life loss reserving constitutes a categorized linear regression. I’ll emphasize that the idea of a linear regression isn’t remotely novel. Further, the categorization is the de facto approach. I’m merely recognizing it and suggesting instances where a decision may be made about the optimality of the categorization.
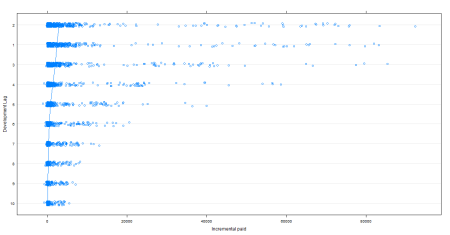
Anyway. I prepared some data to have a bit of fun with. This is taken from the NAIC data set hosted on the CAS website. I’ve combined the results of several different lines for the 27 companies which had results for those lines. The code to construct that dataset may be found in this Gist. Once that’s done, I can look at how incremental paid varies, presuming that the development age constitutes the random effects.
dotplot(reorder(DevInteger, IncrementalPaid) ~ IncrementalPaid, df,
ylab = "Development Lag", jitter.y = TRUE, pch = 21,
xlab = "Incremental paid",
type = c("p", "a"))
That produces this lovely picture:
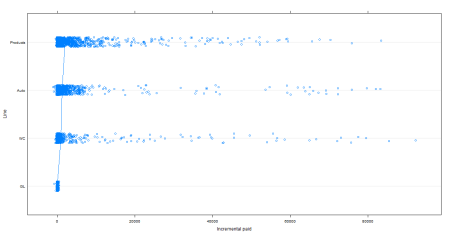
Now the fun stuff. How does incremental paid loss vary by line of business and company?

No surprise that some companies have a great deal more variance than others. For those in the bottom half of the chart, one could probably increase predictive power by combining data across companies.
The small variation and low mean for GL is quite surprising. For the others, the consistency in scale and variance, suggests that it may make sense to combine these lines. I’ll delve into that in a subsequent post.
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.