Complex arithmetic and airplane wings

I was once told that the reason that such a shape was so commonly used for aeroplane wings was merely that then one could study it mathemtically by just employing the Zhoukowski transformation. I hope that this is not true!

(R. Penrose, “The Road to Reality”, p.150)

Penrose here talks about a complex holomorphic mapping also known as the aerofoil transformation.

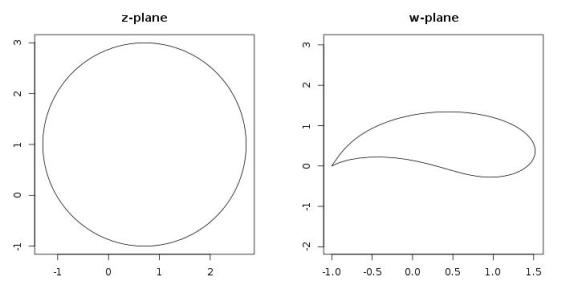
What you need is a cirlce in the complex plane, described by the complex function , that passes through the point . Then the transformation

transforms this circle into the cross section of an airplane wing.

Let’s look at this in R. Fortunately, R has some complex number arithmetic already built in. A suitable circle is constructed by

z <- complex(mod=2,argument=seq(0,2*pi,len=100))+(sqrt(0.5)+1i)

and the plot below (Fig. 8.15 in “Road to Reality”) is produced by

par(mfrow=c(1,2),mar=rep(3,4))
plot(z,type="l",asp=1,main="z-plane")
plot((z+1/z)/2,type="l",main="w-plane",asp=0.5)

Maybe at some point I also understand what Penrose means by

… the (idealized) airflow around [the wing] can be directly obtained from that around a ‘wing’ of circular cross-section

Is it true that a vector field on the surface of the circle directly transforms into the wind field around the wing? How do you transform a vector field by the above equation? Does the transformed wind field explain why the plane flies? Would be nice indeed, but this is another post.