24 Days of R: Day 8
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
I saved the data from the last post which shows the percentage of Republican voters in each county. In addition to that column, I also have figures from the 2010 census. This will show things like age, ethnicity, urbanization and home ownership. Those census figures show actual population counts, so they'll need to be altered to relative numbers to be used in any statistical inference. This will necessitate a read through the obscure column names in the data frame. The USCensus package documents this well.
I'll note two things about the ethnic categories: 1) in pretty much every society on earth, race is a very sensitive, divisive issue with a great deal of history. I'll add the hopelessly needless caveat that although it may be used in a statistical model, that shouldn't suggest that ethnicity connotes any constraints around a person's behavior or ability. 2) Perhaps in conjunction with point 1, the US Census has a very dense set of data collection for race. I'm not going to try to sort through all of the nuance that's captured in the data, but will simply create one data element to capture the percentage of the population which identifies as white, as described in one of the several categories where it is possible to do so.
Everybody cool? Good, let's do some math.
dfNC = read.csv("./Data/NC2012andCensus.csv", stringsAsFactors = FALSE)
dfNC$PctUrban = dfNC$P0020002/dfNC$P0020001
dfNC$PctWhite = dfNC$P0060002/dfNC$P0060001
dfNC$PctVacantHousing = dfNC$H0030003/dfNC$H0030001
dfNC$PctRent = dfNC$H0110004/dfNC$H0110001
dfNC$PctLargeFamily = (dfNC$H0130007 + dfNC$H0130008)/dfNC$H0130001
dfNC$PctOver65 = (dfNC$H0170009 + dfNC$H0170010 + dfNC$H0170011 + dfNC$H0170019 +
dfNC$H0170020 + dfNC$H0170021)/dfNC$H0170001
dfNC$PctWithChildren = (dfNC$H0190003 + dfNC$H0190006)/dfNC$H0190001
keepCols = c("NAME10", "PctRed", "PctUrban", "PctWhite", "PctVacantHousing",
"PctRent", "PctLargeFamily", "PctOver65", "PctWithChildren")
keepCols %in% colnames(dfNC)
## [1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
dfTest = dfNC[, colnames(dfNC) %in% keepCols]
colnames(dfTest)[1] = "CountyName"
head(dfTest)
## CountyName PctRed PctUrban PctWhite PctVacantHousing PctRent
## 1 Franklin 0.5209 0 0.6611 0.1337 0.2578
## 2 Carteret 0.7069 0 0.8918 0.4008 0.2796
## 3 Davidson 0.7069 0 0.8431 0.1120 0.2736
## 4 Sampson 0.5553 0 0.5705 0.1186 0.3053
## 5 Johnston 0.6405 0 0.7433 0.0853 0.2713
## 6 Caldwell 0.6812 0 0.9019 0.1134 0.2739
## PctLargeFamily PctOver65 PctWithChildren
## 1 0.03879 0.2151 0.3457
## 2 0.01791 0.2872 0.2594
## 3 0.02852 0.2380 0.3384
## 4 0.04528 0.2513 0.3560
## 5 0.04334 0.1808 0.4034
## 6 0.02690 0.2542 0.3237
Unfortunately, the urbanization column isn't available for this data. That's a shame as I would imagine that it's very predictive. Later, I'll try to find it elsewhere, or create a proxy variable by computing a population density value.
plot(dfNC$PctWhite, dfNC$PctRed, pch = 19, ylab = "% Red", xlab = "% White")

plot(dfNC$PctVacantHousing, dfNC$PctRed, pch = 19, ylab = "% Red", xlab = "% Vacant")

plot(dfNC$PctRent, dfNC$PctRed, pch = 19, ylab = "% Red", xlab = "% Rent")

plot(dfNC$PctOver65, dfNC$PctRed, pch = 19, ylab = "% Red", xlab = "% Over 65")
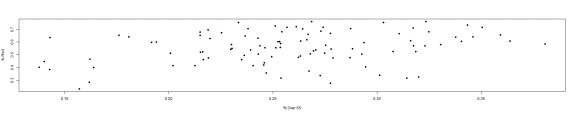
plot(dfNC$PctWithChildren, dfNC$PctRed, pch = 19, ylab = "% Red", xlab = "% w/Children")

plot(dfNC$PctLargeFamily, dfNC$PctRed, pch = 19, ylab = "% Red", xlab = "% Large family")
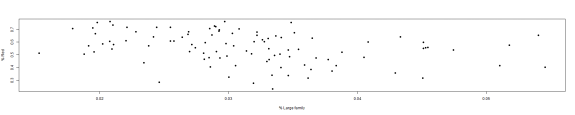
fitAll = lm(PctRed ~ PctWhite + PctVacantHousing + PctRent + PctOver65 + PctWithChildren +
PctLargeFamily, data = dfNC)
summary(fitAll)
##
## Call:
## lm(formula = PctRed ~ PctWhite + PctVacantHousing + PctRent +
## PctOver65 + PctWithChildren + PctLargeFamily, data = dfNC)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.16169 -0.02332 0.00917 0.03686 0.10555
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.8416 0.1761 -4.78 6.6e-06 ***
## PctWhite 0.6432 0.0503 12.78 < 2e-16 ***
## PctVacantHousing 0.0747 0.0676 1.11 0.27
## PctRent 0.1277 0.1473 0.87 0.39
## PctOver65 1.2241 0.2134 5.74 1.2e-07 ***
## PctWithChildren 1.9385 0.3271 5.93 5.2e-08 ***
## PctLargeFamily -1.2827 1.4037 -0.91 0.36
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.0539 on 93 degrees of freedom
## Multiple R-squared: 0.823, Adjusted R-squared: 0.811
## F-statistic: 71.9 on 6 and 93 DF, p-value: <2e-16
The plots would suggest that counties with a large population of rentals are less apt to vote Republican. However, both the sign of the relationship and its significance aren't what we'd expect when we include all variables. I'm going to change the column a bit, so that it's percentage of owne homes and drop a few of the insignificant variables and try the fit again.
dfNC$PctOwn = 1 - dfNC$PctRent fitTwo = lm(PctRed ~ PctWhite + PctOver65 + PctWithChildren + PctOwn, data = dfNC) summary(fitTwo) ## ## Call: ## lm(formula = PctRed ~ PctWhite + PctOver65 + PctWithChildren + ## PctOwn, data = dfNC) ## ## Residuals: ## Min 1Q Median 3Q Max ## -0.16819 -0.02356 0.00769 0.03414 0.10591 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -0.6648 0.0961 -6.92 5.3e-10 *** ## PctWhite 0.6689 0.0440 15.22 < 2e-16 *** ## PctOver65 1.1699 0.2071 5.65 1.7e-07 *** ## PctWithChildren 1.6389 0.2163 7.58 2.3e-11 *** ## PctOwn -0.1081 0.1456 -0.74 0.46 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.0539 on 95 degrees of freedom ## Multiple R-squared: 0.819, Adjusted R-squared: 0.812 ## F-statistic: 108 on 4 and 95 DF, p-value: <2e-16
Ownership continues to show up as insignificant, which is just odd. One final fit with only that variable.
fitOwnership = lm(PctRed ~ PctOwn, data = dfNC) summary(fitOwnership) ## ## Call: ## lm(formula = PctRed ~ PctOwn, data = dfNC) ## ## Residuals: ## Min 1Q Median 3Q Max ## -0.24927 -0.06770 0.00595 0.06981 0.24842 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -0.326 0.115 -2.82 0.0058 ** ## PctOwn 1.240 0.162 7.66 1.3e-11 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.0986 on 98 degrees of freedom ## Multiple R-squared: 0.375, Adjusted R-squared: 0.368 ## F-statistic: 58.8 on 1 and 98 DF, p-value: 1.31e-11
OK. On its own it's fine, but it gets lost when mixed with the other variables.
What does all of this mean? It means that- for this set of explanatory variables and construction of data- absent any significant demographic shifts we can probably expect North Carolina to remain red. An influx of non-white residents, or younger residents could alter that. I'll emphasize that this is a very superficial treatment of complex phenomena. In a later post, I'll augment the basic census data with other data elements. Further, I'll try to fetch data for other states to see how the relationships observed here play out elsewhere in the country.
This is also the part where I point out that Nate Silver and Andrew Gelman- two people who are reliably smarter than I am- have written about political forescasting in a way that I can't hope to replicate. I've read their stuff and it's tremensous. You should do the same.
citation("UScensus2010county")
##
## To cite UScensus2000 in publications use:
##
## Zack W. Almquist (2010). US Census Spatial and Demographic Data
## in R: The UScensus2000 Suite of Packages. Journal of Statistical
## Software, 37(6), 1-31. URL http://www.jstatsoft.org/v37/i06/.
##
## A BibTeX entry for LaTeX users is
##
## @Article{,
## title = {US Census Spatial and Demographic Data in {R}: The {UScensus2000} Suite of Packages},
## author = {Zack W. Almquist},
## journal = {Journal of Statistical Software},
## year = {2010},
## volume = {37},
## number = {6},
## pages = {1--31},
## url = {http://www.jstatsoft.org/v37/i06/},
## }
sessionInfo()
## R version 3.0.2 (2013-09-25)
## Platform: x86_64-w64-mingw32/x64 (64-bit)
##
## locale:
## [1] LC_COLLATE=English_United States.1252
## [2] LC_CTYPE=English_United States.1252
## [3] LC_MONETARY=English_United States.1252
## [4] LC_NUMERIC=C
## [5] LC_TIME=English_United States.1252
##
## attached base packages:
## [1] stats graphics grDevices utils datasets methods base
##
## other attached packages:
## [1] RWordPress_0.2-3 UScensus2010county_1.00 UScensus2010_0.11
## [4] foreign_0.8-55 maptools_0.8-27 reshape2_1.2.2
## [7] knitr_1.4.1 sp_1.0-13
##
## loaded via a namespace (and not attached):
## [1] digest_0.6.3 evaluate_0.4.7 formatR_0.9 grid_3.0.2
## [5] lattice_0.20-23 plyr_1.8 RCurl_1.95-4.1 stringr_0.6.2
## [9] tools_3.0.2 XML_3.98-1.1 XMLRPC_0.3-0
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
