The little mixed model that could, but shouldn’t be used to score surgical performance
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
The Surgeon Scorecard
Two weeks ago, the world of medical journalism was rocked by the public release of ProPublica’s Surgeon Scorecard. In this project ProPublica “calculated death and complication rates for surgeons performing one of eight elective procedures in Medicare, carefully adjusting for differences in patient health, age and hospital quality.” By making the dataset available through a user friendly portal, the intended use of this public resource was to “use this database to know more about a surgeon before your operation“.
The Scorecard was met with great enthusiasm and coverage by non-medical media. TODAY.com headline “nutshelled” the Scorecard as a resource that “aims to help you find doctors with lowest complication rates“. A (?tongue in cheek) NBC headline tells us the scorecard “It’s complicated“. On the other hand the project was not well received by my medical colleagues. John Mandrola gave it a failing grade in Medscape. Writing at KevinMD.com, Jeffrey Parks called it a journalistic low point for ProPublica. Jha Shaurabh pointed out a potential paradox in a statistically informed, easy to read and highly entertaining piece. In this paradox, the surgeon with the higher complication case who takes high risk patients from a disadvantaged socio-economic environment, may actually be the surgeon one wants to perform one’s surgery! Ed Schloss summarized the criticism (in the blogosphere and twitter) in an open letter and asked for peer review of the Scorecard methodology.
The criticism to date has largely focused on the potential for selection effects (as the Scorecard is based on Medicare data, and does not include data from private insurers), the incomplete adjustment for confounders, the paucity of data for individual surgeons, the counting of complications and re-admission rates, decisions about risk category classification boundaries and even data errors (ProPublica’s response arguing that the Scorecard matters may be found here). With a few exceptions (e.g. see Schloss’s blogpost in which the complexity of the statistical approach is mentioned) the criticism of the statistical approach (including my own comments in twitter) has largely focused on these issues.
On the other hand, the underlying statistical methodology (here and there) that powers the Scorecard has not received much attention. Therefore I undertook a series of simulation experiments to explore the impact of the statistical procedures on the inferences afforded by the Scorecard.
The mixed model that could – a short non-technical summary of ProPublica’s approah
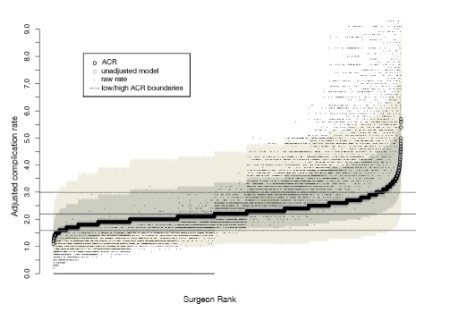
ProPublica’s approach to the scorecard is based on logistic regression model, in which individual surgeon (and hospital) performance (probability of suffering a complication) is modelled using Gaussian random effects, while patient level characteristics that may act as confounders are adjusted for, using fixed effects. In a nutshell this approach implies fitting a model of the average complication rate that is function of the fixed effects (e.g. patient age) for the entire universe of surgeries performed in the USA. Individual surgeon and hospital factors modify this complication rate, so that a given surgeon and hospital will have an individual rate that varies around the population average. These individual surgeon and hospital factors are constrained to follow Gaussian, bell-shaped distribution when analyzing complication data. After model fitting, these predicted random effects are used to quantify and compare surgical performance. A feature of mixed modeling approaches is the unavoidable shrinkage of the raw complication rate towards the population mean. Shrinkage implies that the dynamic range of the actually observed complication rates is compressed. This is readily appreciated in the figures generated by the ProPublica analytical team:
In their methodological white paper the ProPublica team notes:
“While raw rates ranged from 0.0 to 29%, the Adjusted Complication Rate goes from 1.1 to 5.7%. …. shrinkage is largely a result of modeling in the first place, not due to adjusting for case mix. This shrinkage is another piece of the measured approach we are taking: we are taking care not to unfairly characterize surgeons and hospitals.”
These features should alert us that something is going on. For if a model can distort the data to such a large extent, then the model should be closely scrutinized before being accepted. In fact, given these observations, it is possible that one mistakes the noise from the model for the information hidden in the empirical data. Or, even more likely, that one is not using the model in the most productive manner.
Note that these comments should not be interpreted as a criticism against the use of mixed models in general, or even for the particular aspects of the Scorecard project. They are rather a call for re-examining the modeling assumptions and for gaining a better understanding of the model “mechanics of prediction” before releasing the Kraken to the world.
The little mixed model that shouldn’t
There are many technical aspects one could potentially misfire in a Generalized Linear Mixed Model for complication rates. Getting the wrong shape of the random effects distribution is of concern (e.g. assuming it is bell shaped when it is not). Getting the underlying model wrong, e.g. assuming the binomial model for complication rates while a model with many more zeros (a zero inflated model) may be more appropriate, is yet another potential problem area. However, even if these factors are not operational, then one may still be misled when using the results of the model. In particular, the major area of concern for such models is the cluster size: the number of observations per individual random effect (e.g. surgeon) in the dataset. It is this factor, rather than the actual size of the dataset that determines the precision in the individual random affects. Using a toy example, we show that the number of observations per surgeon typical of the Scorecard dataset, leads to predicted random effects that may be far from their true value. This seems to stem from the non-linear nature of the logistic regression model. As we conclude in our first technical post:
- Random Effect modeling of binomial outcomes require a substantial number of observations per individual (in the order of thousands) for the procedure to yield estimates of individual effects that are numerically indistinguishable from the true values.
Contrast this conclusion to the cluster size in the actual scorecard:
| Procedure Code | N (procedures) | N(surgeons) | Procedures per surgeon |
| 51.23 | 201,351 | 21,479 | 9.37 |
| 60.5 | 78,763 | 5,093 | 15.46 |
| 60.29 | 73,752 | 7,898 | 9.34 |
| 81.02 | 52,972 | 5,624 | 9.42 |
| 81.07 | 106,689 | 6,214 | 17.17 |
| 81.08 | 102,716 | 6,136 | 16.74 |
| 81.51 | 494,576 | 13,414 | 36.87 |
| 81.54 | 1,190,631 | 18,029 | 66.04 |
| Total | 2,301,450 | 83,887 | 27.44 |
In a follow up simulation study we demonstrate that this feature results in predicted individual effects that are non-uniformly shrank towards their average value. This compromises the ability of mixed model predictions to separate the good from the bad “apples”.
In the second technical post, we undertook a simulation study to understand the implications of over-shrinkage for the Scorecard project. These are best understood by a numerical example from one of simulated datasets. To understand this example one should note that the individual random effects have the interpretation of (log-) odds ratios. Hence, the difference in these random effects when exponentiated yield the odds ratio of suffering a complication in the hands of a good relative to a bad surgeon. By comparing these random effects for good and bad surgeons who are equally bad (or good) relative to the mean (symmetric quantiles around the median), one can get an idea of the impact of using the predicted random effects to carry out individual comparisons.
| Good | Bad | Quantile (Good) | Quantile (Bad) | True OR | Pred OR | Shrinkage Factor |
| -0.050 | 0.050 | 48.0 | 52.0 | 0.905 | 0.959 | 1.06 |
| -0.100 | 0.100 | 46.0 | 54.0 | 0.819 | 0.920 | 1.12 |
| -0.150 | 0.150 | 44.0 | 56.0 | 0.741 | 0.883 | 1.19 |
| -0.200 | 0.200 | 42.1 | 57.9 | 0.670 | 0.847 | 1.26 |
| -0.250 | 0.250 | 40.1 | 59.9 | 0.607 | 0.813 | 1.34 |
| -0.300 | 0.300 | 38.2 | 61.8 | 0.549 | 0.780 | 1.42 |
| -0.350 | 0.350 | 36.3 | 63.7 | 0.497 | 0.749 | 1.51 |
| -0.400 | 0.400 | 34.5 | 65.5 | 0.449 | 0.719 | 1.60 |
| -0.450 | 0.450 | 32.6 | 67.4 | 0.407 | 0.690 | 1.70 |
| -0.500 | 0.500 | 30.9 | 69.1 | 0.368 | 0.662 | 1.80 |
| -0.550 | 0.550 | 29.1 | 70.9 | 0.333 | 0.635 | 1.91 |
| -0.600 | 0.600 | 27.4 | 72.6 | 0.301 | 0.609 | 2.02 |
| -0.650 | 0.650 | 25.8 | 74.2 | 0.273 | 0.583 | 2.14 |
| -0.700 | 0.700 | 24.2 | 75.8 | 0.247 | 0.558 | 2.26 |
| -0.750 | 0.750 | 22.7 | 77.3 | 0.223 | 0.534 | 2.39 |
| -0.800 | 0.800 | 21.2 | 78.8 | 0.202 | 0.511 | 2.53 |
| -0.850 | 0.850 | 19.8 | 80.2 | 0.183 | 0.489 | 2.68 |
| -0.900 | 0.900 | 18.4 | 81.6 | 0.165 | 0.467 | 2.83 |
| -0.950 | 0.950 | 17.1 | 82.9 | 0.150 | 0.447 | 2.99 |
| -1.000 | 1.000 | 15.9 | 84.1 | 0.135 | 0.427 | 3.15 |
| -1.050 | 1.050 | 14.7 | 85.3 | 0.122 | 0.408 | 3.33 |
| -1.100 | 1.100 | 13.6 | 86.4 | 0.111 | 0.390 | 3.52 |
| -1.150 | 1.150 | 12.5 | 87.5 | 0.100 | 0.372 | 3.71 |
| -1.200 | 1.200 | 11.5 | 88.5 | 0.091 | 0.356 | 3.92 |
| -1.250 | 1.250 | 10.6 | 89.4 | 0.082 | 0.340 | 4.14 |
| -1.300 | 1.300 | 9.7 | 90.3 | 0.074 | 0.325 | 4.37 |
| -1.350 | 1.350 | 8.9 | 91.1 | 0.067 | 0.310 | 4.62 |
| -1.400 | 1.400 | 8.1 | 91.9 | 0.061 | 0.297 | 4.88 |
| -1.450 | 1.450 | 7.4 | 92.6 | 0.055 | 0.283 | 5.15 |
| -1.500 | 1.500 | 6.7 | 93.3 | 0.050 | 0.271 | 5.44 |
| -1.550 | 1.550 | 6.1 | 93.9 | 0.045 | 0.259 | 5.74 |
| -1.600 | 1.600 | 5.5 | 94.5 | 0.041 | 0.247 | 6.07 |
| -1.650 | 1.650 | 4.9 | 95.1 | 0.037 | 0.236 | 6.41 |
| -1.700 | 1.700 | 4.5 | 95.5 | 0.033 | 0.226 | 6.77 |
| -1.750 | 1.750 | 4.0 | 96.0 | 0.030 | 0.216 | 7.14 |
| -1.800 | 1.800 | 3.6 | 96.4 | 0.027 | 0.206 | 7.55 |
| -1.850 | 1.850 | 3.2 | 96.8 | 0.025 | 0.197 | 7.97 |
| -1.900 | 1.900 | 2.9 | 97.1 | 0.022 | 0.188 | 8.42 |
| -1.950 | 1.950 | 2.6 | 97.4 | 0.020 | 0.180 | 8.89 |
| -2.000 | 2.000 | 2.3 | 97.7 | 0.018 | 0.172 | 9.39 |
| -2.050 | 2.050 | 2.0 | 98.0 | 0.017 | 0.164 | 9.91 |
From this table it can be seen that predicted odds ratios are always larger than the true ones. The ratio of these odds ratios (the shrinkage factor) is larger, the more extreme comparisons are contemplated.
In summary, the use of the random effects models for the small cluster sizes (number of observations per surgeon) is likely to lead to estimates (or rather predictions) of individual effects that are smaller than their true values. Even though one should expect the differences to decrease with larger cluster sizes, this is unlikely to happen in real world datasets (how often does one come across a surgeon who has performed 1000s of operation of the same type before they retire?). Hence, the comparison of surgeon performance based on these random effect predictions is likely to be misleading due to over-shrinkage.
Where to go from here?
ProPublica should be congratulated for taking up such an ambitious, and ultimately useful project. However, the limitations of the adopted approach should make one very skeptical about accepting the inferences from their modeling tool. In particular, the small number of observations per surgeon limits the utility of the predicted random effects to directly compare surgeons due to over-shrinkage. Further studies are required before one could use the results of mixed effects modeling for this application. Based on some limited simulation experiments (that we do not present here), it seems that relative rankings of surgeons may be robust measures of surgical performance, at least compared to the absolute rates used by the Scorecard. Adding my voice to that of Dr Schloss, I think it is time for an open and transparent dialogue (and possibly a “crowdsourced” research project) to better define the best measure of surgical performance given the limitations of the available data. Such a project could also explore other directions, e.g. the explicit handling of zero inflation and even go beyond the ubiquitous bell shaped curve. By making the R code available, I hope that someone (possibly ProPublica) who can access more powerful computational resources can perform more extensive simulations. These may better define other aspects of the modeling approach and suggest improvements in the scorecard methodology. In the meantime, it is probably a good idea not to exclusively rely on the numerical measures of the scorecard when picking up the surgeon who will perform your next surgery.
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.