Sampling paths from a Gaussian process
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
Gaussian processes are a widely employed statistical tool because of their flexibility and computational tractability. (For instance, one recent area where Gaussian processes are used is in machine learning for hyperparameter optimization.)
A stochastic process is a Gaussian process if (and only if) any finite subcollection of random variables
has a multivariate Gaussian distribution. Here,
is the index set for the Gaussian process; most often we have
(to index time) or
(to index space).
The stochastic nature of Gaussian processes also allows it to be thought of as a distribution over functions. One draw from a Gaussian process over corresponds to choosing a function according to some probability distribution over these functions.
Gaussian processes are defined by their mean and covariance functions. The covariance (or kernel) function is what characterizes the shapes of the functions which are drawn from the Gaussian process. In this post, we will demonstrate how the choice of covariance function affects the shape of functions it produces. For simplicity, we will assume
.
(Click on this link to see all code for this post in one script. For more technical details on the covariance functions, see this previous post.)
Overall set-up
Let’s say we have a zero-centered Gaussian process denoted by , and that
is a function drawn from this Gaussian process. For a vector
, the function values
must have a multivariate Gaussian distribution with mean
and covariance matrix
with entries
. We make use of this property to draw this function: we select a fine grid of x-coordinates, use
mvrnorm() from the MASS package to draw the function values at these points, then connect them with straight lines.
Assume that we have already written an R function kernel_fn for the kernel. The first function below generates a covariance matrix from this kernel, while the second takes N draws from this kernel (using the first function as a subroutine):
library(MASS)
# generate covariance matrix for points in `x` using given kernel function
cov_matrix <- function(x, kernel_fn, ...) {
outer(x, x, function(a, b) kernel_fn(a, b, ...))
}
# given x coordinates, take N draws from kernel function at those points
draw_samples <- function(x, N, seed = 1, kernel_fn, ...) {
Y <- matrix(NA, nrow = length(x), ncol = N)
set.seed(seed)
for (n in 1:N) {
K <- cov_matrix(x, kernel_fn, ...)
Y[, n] <- mvrnorm(1, mu = rep(0, times = length(x)), Sigma = K)
}
Y
}
The ... argument for the draw_samples() function allows us to pass arguments into the kernel function kernel_fn.
We will use the following parameters for the rest of the post:
x <- seq(0, 2, length.out = 201) # x-coordinates
N <- 3 # no. of draws
col_list <- c("red", "blue", "black") # for line colors
Squared exponential (SE) kernel
The squared exponential (SE) kernel, also known as the radial basis function (RBF) kernel or the Gaussian kernel has the form
where and
se_kernel <- function(x, y, sigma = 1, length = 1) {
sigma^2 * exp(- (x - y)^2 / (2 * length^2))
}
Y <- draw_samples(x, N, kernel_fn = se_kernel, length = 0.2)
plot(range(x), range(Y), xlab = "x", ylab = "y", type = "n",
main = "SE kernel, length = 0.2")
for (n in 1:N) {
lines(x, Y[, n], col = col_list[n], lwd = 1.5)
}
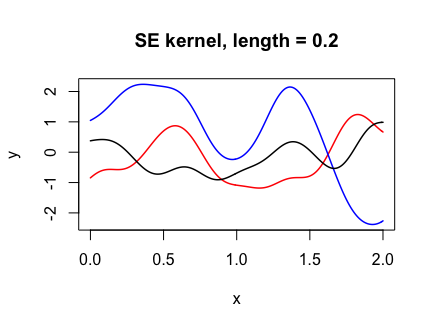

The following code shows how changing the “length-scale” parameter l affects the functions drawn. The smaller l is, the more wiggly the functions drawn.
par(mfrow = c(1, 3))
for (l in c(0.2, 0.7, 1.5)) {
Y <- draw_samples(x, N, kernel_fn = se_kernel, length = l)
plot(range(x), range(Y), xlab = "x", ylab = "y", type = "n",
main = paste("SE kernel, length =", l))
for (n in 1:N) {
lines(x, Y[, n], col = col_list[n], lwd = 1.5)
}
}


Rational quadratic (RQ) kernel
The rational quadratic (RQ) kernel has the form
where and
are hyperparameters. Below we create a function for the kernel and demonstrate how
l affects the functions drawn:
rq_kernel <- function(x, y, alpha = 1, sigma = 1, length = 1) {
sigma^2 * (1 + (x - y)^2 / (2 * alpha * length^2))^(-alpha)
}
par(mfrow = c(1, 3))
for (a in c(0.01, 0.5, 50)) {
Y <- draw_samples(x, N, kernel_fn = rq_kernel, alpha = a)
plot(range(x), range(Y), xlab = "x", ylab = "y", type = "n",
main = paste("RQ kernel, alpha =", a))
for (n in 1:N) {
lines(x, Y[, n], col = col_list[n], lwd = 1.5)
}
}


Matérn covariance functions
The Matérn covariance function has the form
where and
matern_kernel <- function(x, y, nu = 1.5, sigma = 1, l = 1) {
if (!(nu %in% c(0.5, 1.5, 2.5))) {
stop("p must be equal to 0.5, 1.5 or 2.5")
}
p <- nu - 0.5
d <- abs(x - y)
if (p == 0) {
sigma^2 * exp(- d / l)
} else if (p == 1) {
sigma^2 * (1 + sqrt(3)*d/l) * exp(- sqrt(3)*d/l)
} else {
sigma^2 * (1 + sqrt(5)*d/l + 5*d^2 / (3*l^2)) * exp(-sqrt(5)*d/l)
}
}
par(mfrow = c(1, 3))
for (nu in c(0.5, 1.5, 2.5)) {
Y <- draw_samples(x, N, kernel_fn = matern_kernel, nu = nu)
plot(range(x), range(Y), xlab = "x", ylab = "y", type = "n",
main = paste("Matern kernel, nu =", nu * 2, "/ 2"))
for (n in 1:N) {
lines(x, Y[, n], col = col_list[n], lwd = 1.5)
}
}


The paths from the Matérn-1/2 kernel are often deemed too rough to be used in practice.
Periodic kernel
The periodic kernel has the form
where and
are hyperparameters. It is good for modeling functions which repeat themselves exactly.
period_kernel <- function(x, y, p = 1, sigma = 1, length = 1) {
sigma^2 * exp(-2 * sin(pi * abs(x - y) / p)^2 / length^2)
}
par(mfrow = c(1, 3))
for (p in c(0.5, 1, 2)) {
Y <- draw_samples(x, N, kernel_fn = period_kernel, p = p)
plot(range(x), range(Y), xlab = "x", ylab = "y", type = "n",
main = paste("Periodic kernel, p =", p))
for (n in 1:N) {
lines(x, Y[, n], col = col_list[n], lwd = 1.5)
}
}


Linear/polynomial kernel
The polynomial kernel has the form
where
poly_kernel <- function(x, y, sigma = 1, d = 1) {
(sigma^2 + x * y)^d
}
# linear kernel w different sigma
par(mfrow = c(1, 3))
for (s in c(0.5, 1, 5)) {
Y <- draw_samples(x, N, kernel_fn = poly_kernel, sigma = s)
plot(range(x), range(Y), xlab = "x", ylab = "y", type = "n",
main = paste("Linear kernel, sigma =", s))
for (n in 1:N) {
lines(x, Y[, n], col = col_list[n], lwd = 1.5)
}
}
# poly kernel of different dimensions
par(mfrow = c(1, 3))
for (d in c(1, 2, 3)) {
Y <- draw_samples(x, N, kernel_fn = poly_kernel, d = d)
plot(range(x), range(Y), xlab = "x", ylab = "y", type = "n",
main = paste("Polynomial kernel, d =", d))
for (n in 1:N) {
lines(x, Y[, n], col = col_list[n], lwd = 1.5)
}
}




Brownian motion
Brownian motion, the most studied object in stochastic processes, is a one-dimensional Gaussian process with mean zero and covariance function
bm_kernel <- function(x, y) {
pmin(x, y)
}
Y <- draw_samples(x, N, kernel_fn = bm_kernel)
plot(range(x), range(Y), xlab = "x", ylab = "y", type = "n",
main = "Brownian motion kernel")
for (n in 1:N) {
lines(x, Y[, n], col = col_list[n], lwd = 1.5)
}
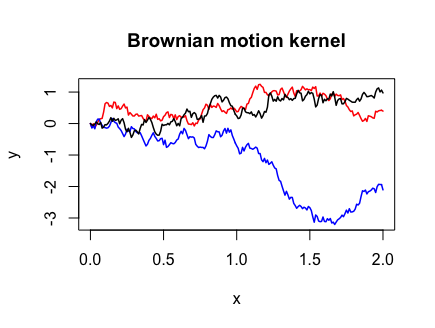

Note that I had to use the pmin() function instead of min() in the Brownian motion covariance function. This is because the outer(X, Y, FUN, ...) function we called in cov_matrix()
“…[extends
XandY] byrepto length the products of the lengths ofXandYbeforeFUNis called.” (fromouter()documentation)
pmin() would perform the operation we want, while min() would simply return the minimum value present in the two arguments, not what we want.
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
