Creating landscapes and simulating species occupation with MetaLandSim
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
MetaLandSim is an R package I’ve developed to simulate metapopulational dynamics on an habitat network. It also computes a lot of landscape connectivity metrics and simulates range expansion (check the manual if you are interested).
I’ve mentioned it here frequently, and sometimes I like to post a simple script that I used to answer a user’s question, or a that I’ve written for any other reason. This is a run through the main functions of the package.
Much more complex uses are possible, and I’ve already published a paper with some advanced uses of the package (with another one on the way – I hope!).
Let’s start!
First of all, as always, we should load the package:
# load the package library(MetaLandSim) ## Warning: package 'MetaLandSim' was built under R version 3.5.1 ## Loading required package: tcltk ## Loading required package: igraph ## Warning: package 'igraph' was built under R version 3.5.1 ## ## Attaching package: 'igraph' ## The following objects are masked from 'package:stats': ## ## decompose, spectrum ## The following object is masked from 'package:base': ## ## union
Now, to create a random landscape of 10 patches with mean area of 0.2 hectares, and with the landscape mosaic being a square with 1000 meters side.
The species mean dispersal ability is 120 meters (this is merely for graphical purposes, in order to connect the patches producing the graph).
A plot with the landscape graph is displayed graphically.
So… let’s create the landscape:
# set up the plotting window
plot.new()
par(mfrow = c(1,2))
set.seed(200)
rl1 <- rland.graph(mapsize = 1000,
dist_m = 80,
areaM = 0.2,
areaSD = 0.115,
Npatch = 10,
disp = 120,
plotG = TRUE)
# look at the node.characteristics
nodes <- rl1$nodes.characteristics
nodes
And this data frame shows the characteristics of each patch:
## x y areas radius cluster colour nneighbour ID ## 1 533.7724 583.76503 0.18420882 24.214766 1 #FF0000FF 102.9282 1 ## 2 454.3649 649.25291 0.10651184 18.412977 1 #FF0000FF 102.9282 2 ## 3 589.5783 691.03989 0.04015217 11.305234 2 #FFBF00FF 120.9222 3 ## 4 667.3315 839.29374 0.08311528 16.265428 3 #80FF00FF 167.4060 4 ## 5 711.6001 96.50122 0.36824823 34.236976 4 #00FF40FF 149.0693 5 ## 6 523.8247 235.35054 0.12806475 20.190165 5 #00FFFFFF 112.1129 6 ## 7 566.7674 131.78785 0.01301267 6.435886 5 #00FFFFFF 112.1129 7 ## 8 153.7271 649.28867 0.28659388 30.203587 6 #0040FFFF 300.6378 8 ## 9 383.2137 307.29806 0.15232900 22.019951 7 #8000FFFF 157.9491 9 ## 10 922.1776 646.32962 0.20853287 25.763943 8 #FF00BFFF 319.6587 10 # label the node points text(x = nodes[,'x'],y = nodes[,'y'], pos = 2, offset = .5, labels = as.character(nodes[,'ID'])) # look at information associated with this object # note the class is a landscape class(rl1) ## [1] "landscape" names(rl1) ## [1] "mapsize" "minimum.distance" "mean.area" ## [4] "SD.area" "number.patches" "dispersal" ## [7] "nodes.characteristics"
In order to look at the structure of the object ‘rl1’, our random landscape (the graph):
str(rl1) ## List of 7 ## $ mapsize : num 1000 ## $ minimum.distance : num 80 ## $ mean.area : num 0.157 ## $ SD.area : num 0.11 ## $ number.patches : int 10 ## $ dispersal : num 120 ## $ nodes.characteristics:'data.frame': 10 obs. of 8 variables: ## ..$ x : num [1:10] 534 454 590 667 712 ... ## ..$ y : num [1:10] 583.8 649.3 691 839.3 96.5 ... ## ..$ areas : num [1:10] 0.1842 0.1065 0.0402 0.0831 0.3682 ... ## ..$ radius : num [1:10] 24.2 18.4 11.3 16.3 34.2 ... ## ..$ cluster : int [1:10] 1 1 2 3 4 5 5 6 7 8 ## ..$ colour : Factor w/ 8 levels "#0040FFFF","#00FF40FF",..: 6 6 8 5 2 3 3 1 4 7 ## ..$ nneighbour: num [1:10] 103 103 121 167 149 ... ## ..$ ID : int [1:10] 1 2 3 4 5 6 7 8 9 10 ## - attr(*, "class")= chr "landscape"
Obtaining the summary of the landscape:
summary_landscape(rl1) ## Value ## landscape area (hectares) 100.000 ## number of patches 10.000 ## mean patch area (hectares) 0.157 ## SD patch area 0.110 ## mean distance amongst patches (meters) 391.228 ## minimum distance amongst patches (meters) 60.300
This landscape is really a mathematical graph, where edges connect nodes (points) if they are within the dispersal distance:
help('edge.graph')
e1 <- edge.graph(rl1)
e1
## ID node A node B area ndA area ndB XA YA XB
## 1 1 2 1 0.10651184 0.1842088 454.3649 649.2529 533.7724
## 2 2 7 6 0.01301267 0.1280648 566.7674 131.7879 523.8247
## YB distance
## 1 583.7650 102.9282
## 2 235.3505 112.1129
And now, let’s populate the patches with a species, considering that red is empty, green is occupied:
help('species.graph')
set.seed(10)
sp_t0 <- species.graph(rl = rl1,
method = "percentage",
parm = 50,
nsew = "none",
plotG = TRUE)
# label the node points
text(x = nodes[,'x'],y = nodes[,'y'], pos = 2, offset = 0.5, labels = as.character(nodes[,'ID']))
This figure shows the empty landscape on the left (rl1) and the occupied on the right (sp_t0):

Look at the information regarding this object. Note the class is metapopulation also note the addition of element ‘distance.to.neighbors’.
Let’s check the class of object ‘sp_t0’:
class(sp_t0) ## [1] "metapopulation" names(sp_t0) ## [1] "mapsize" "minimum.distance" ## [3] "mean.area" "SD.area" ## [5] "number.patches" "dispersal" ## [7] "distance.to.neighbours" "nodes.characteristics"
And now, looking at the structure of ‘sp_t0’:
str(sp_t0) ## List of 8 ## $ mapsize : num 1000 ## $ minimum.distance : num 80 ## $ mean.area : num 0.157 ## $ SD.area : num 0.11 ## $ number.patches : num 10 ## $ dispersal : num 120 ## $ distance.to.neighbours:'data.frame': 10 obs. of 10 variables: ## ..$ 1 : num [1:10] 0 103 121 288 519 ... ## ..$ 2 : num [1:10] 103 0 142 285 610 ... ## ..$ 3 : num [1:10] 121 142 0 167 607 ... ## ..$ 4 : num [1:10] 288 285 167 0 744 ... ## ..$ 5 : num [1:10] 519 610 607 744 0 ... ## ..$ 6 : num [1:10] 349 420 460 621 234 ... ## ..$ 7 : num [1:10] 453 530 560 715 149 ... ## ..$ 8 : num [1:10] 386 301 438 548 785 ... ## ..$ 9 : num [1:10] 315 349 436 603 390 ... ## ..$ 10: num [1:10] 393 468 336 320 589 ... ## $ nodes.characteristics :'data.frame': 10 obs. of 9 variables: ## ..$ x : num [1:10] 534 454 590 667 712 ... ## ..$ y : num [1:10] 583.8 649.3 691 839.3 96.5 ... ## ..$ areas : num [1:10] 0.1842 0.1065 0.0402 0.0831 0.3682 ... ## ..$ radius : num [1:10] 24.2 18.4 11.3 16.3 34.2 ... ## ..$ cluster : int [1:10] 1 1 2 3 4 5 5 6 7 8 ## ..$ colour : Factor w/ 8 levels "#0040FFFF","#00FF40FF",..: 6 6 8 5 2 3 3 1 4 7 ## ..$ nneighbour: num [1:10] 103 103 121 167 149 ... ## ..$ ID : int [1:10] 1 2 3 4 5 6 7 8 9 10 ## ..$ species : num [1:10] 1 0 1 1 1 1 0 0 0 0 ## - attr(*, "class")= chr "metapopulation"
Look at some elements like distance.to.neighbors:
head(sp_t0$distance.to.neighbours, n = 3) ## 1 2 3 4 5 6 7 8 ## 1 0.0000 102.9282 120.9222 288.3278 518.6990 348.5565 453.1799 385.6524 ## 2 102.9282 0.0000 141.5232 285.4300 609.6756 419.6902 529.5323 300.6378 ## 3 120.9222 141.5232 0.0000 167.4060 606.9312 460.4089 559.7171 437.8463 ## 9 10 ## 1 314.8046 393.4118 ## 2 349.2787 467.8218 ## 3 435.7111 335.5909
Note the species column in nodes.characteristics, it contains the information on the presence and absence of the focal species in the habitat network:
sp_t0$nodes.characteristics ## x y areas radius cluster colour nneighbour ID ## 1 533.7724 583.76503 0.18420882 24.214766 1 #FF0000FF 102.9282 1 ## 2 454.3649 649.25291 0.10651184 18.412977 1 #FF0000FF 102.9282 2 ## 3 589.5783 691.03989 0.04015217 11.305234 2 #FFBF00FF 120.9222 3 ## 4 667.3315 839.29374 0.08311528 16.265428 3 #80FF00FF 167.4060 4 ## 5 711.6001 96.50122 0.36824823 34.236976 4 #00FF40FF 149.0693 5 ## 6 523.8247 235.35054 0.12806475 20.190165 5 #00FFFFFF 112.1129 6 ## 7 566.7674 131.78785 0.01301267 6.435886 5 #00FFFFFF 112.1129 7 ## 8 153.7271 649.28867 0.28659388 30.203587 6 #0040FFFF 300.6378 8 ## 9 383.2137 307.29806 0.15232900 22.019951 7 #8000FFFF 157.9491 9 ## 10 922.1776 646.32962 0.20853287 25.763943 8 #FF00BFFF 319.6587 10 ## species ## 1 1 ## 2 0 ## 3 1 ## 4 1 ## 5 1 ## 6 1 ## 7 0 ## 8 0 ## 9 0 ## 10 0
Summarizing the object ‘sp_t0’:
summary_metapopulation(sp_t0) ## Value ## landscape area (hectares) 100.000 ## number of patches 10.000 ## mean patch area (hectares) 0.157 ## SD patch area 0.110 ## mean distance amongst patches (meters) 391.228 ## minimum distance amongst patches (meters) 60.300 ## species occurrence - snapshot 1 50.000
And now, finally, we can simulate the occupation on the next time step (function ”spom’), after defining the parameters setting up the options for the simulation:
# ultimately we need to provide the 'rules' by which patch dynamics occur; notice there several options
help("spom")
# establish parameters that control changes in occupancy through time; here use the built-in dataset that contains the key parameters
help('param1')
data(param1)
# view this object; note the four parameters named alpha, x, y, e; these will be used to control our dynamics
View(param1)
# to simulate dynamics through time, use spom function
# spom stands for stochastic patch occupancy model
help('spom')
sp_t1 <- spom(sp_t0, kern = "op1",
conn = "op1",
colnz = "op1",
ext = "op1",
param_df = param1,
beta1 = NULL,
b = 1,
c1 = NULL,
c2 = NULL,
z = NULL,
R = NULL)
class(sp_t1)
## [1] "list"
The dynamics are contained in the data frame ‘nodes.characteristic’. It depicts the species presence at time step t (species), time step t+1 (species2) and turnover:
head(sp_t1$nodes.characteristics) ## x y areas radius cluster colour nneighbour ID ## 1 533.7724 583.76503 0.18420882 24.21477 1 #FF0000FF 102.9282 1 ## 2 454.3649 649.25291 0.10651184 18.41298 1 #FF0000FF 102.9282 2 ## 3 589.5783 691.03989 0.04015217 11.30523 2 #FFBF00FF 120.9222 3 ## 4 667.3315 839.29374 0.08311528 16.26543 3 #80FF00FF 167.4060 4 ## 5 711.6001 96.50122 0.36824823 34.23698 4 #00FF40FF 149.0693 5 ## 6 523.8247 235.35054 0.12806475 20.19017 5 #00FFFFFF 112.1129 6 ## species species2 turn ## 1 1 1 0 ## 2 0 0 0 ## 3 1 1 0 ## 4 1 1 0 ## 5 1 1 0 ## 6 1 1 0
To simulate the dynamics across multiple steps and get the results use the ‘iterate.graph’ function, which runs the full simulation:
it1 <- iterate.graph(iter = 2,
mapsize = 10000,
dist_m = 10,
areaM = 0.05,
areaSD = 0.02,
Npatch = 250,
disp = 800,
span = 100,
par1 = "hab",
par2 = 2,
par3 = NULL,
par4 = NULL,
par5 = NULL,
method = "percentage",
parm = 50,
nsew = "none",
succ = "none",
param_df = param1,
kern = "op1",
conn = "op1",
colnz = "op1",
ext = "op1",
beta1 = NULL,
b = 1,
c1 = NULL,
c2 = NULL,
z = NULL,
R = NULL,
graph = TRUE)
## Completed iteration 1 of 2
## Completed iteration 2 of 2
Which will open the web browser with the following graphs:
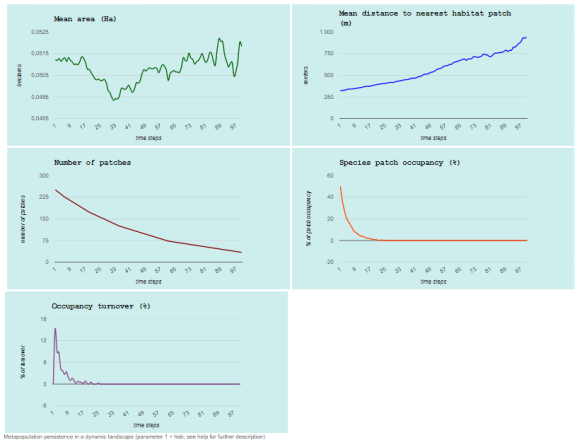
And that’s all for now!
Thanks!
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
