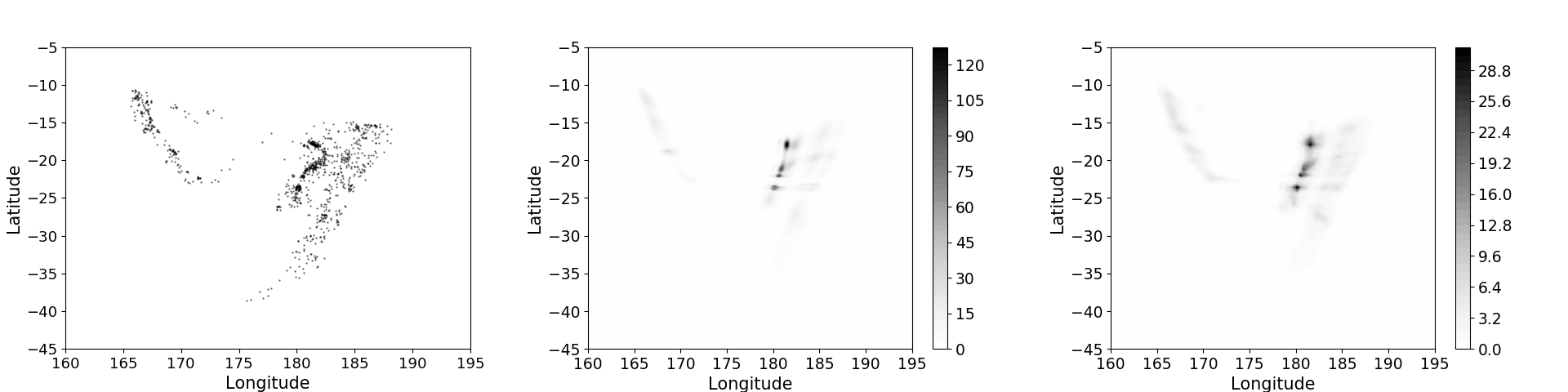
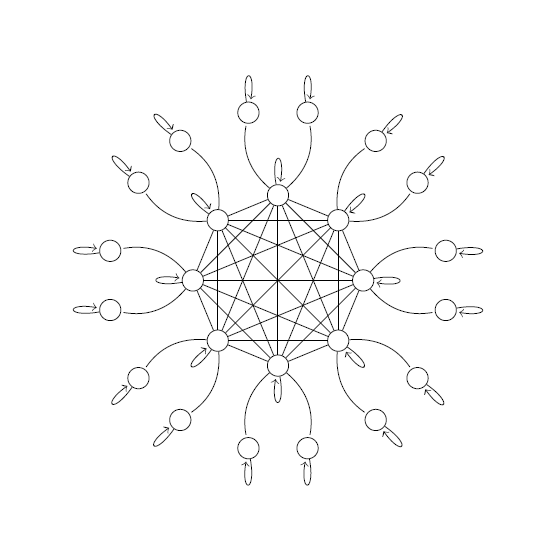
Illustration of Graphical Gaussian Process models to analyze highly multivariate spatial data
Introduction
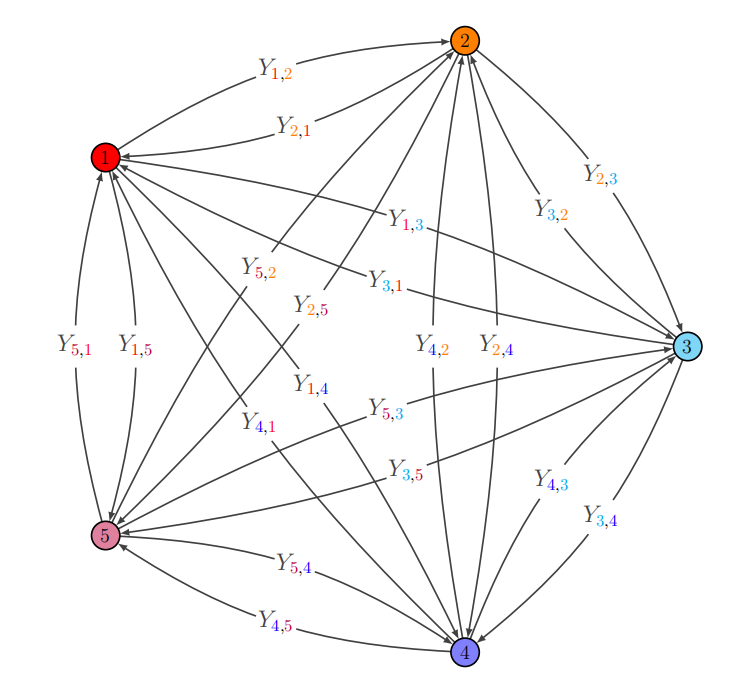
Abundant multivariate spatial data from the natural and environmental sciences demands research on the joint distribution of multiple spatially dependent variables (Wackernagel (2013), Cressie and Wikle (2011), Banerjee and Gelfand (2014)). Here, our goal is to estimate associations over spatial locations for each variable and those among the variables.
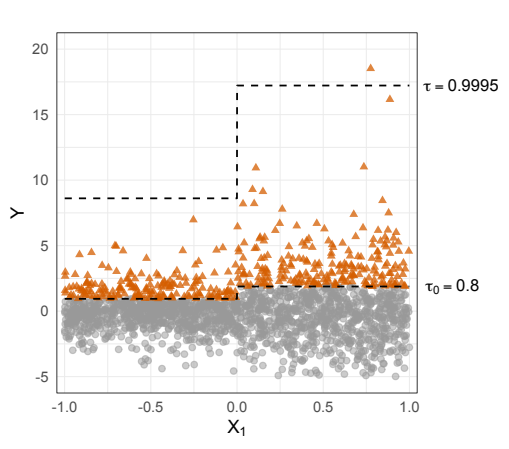
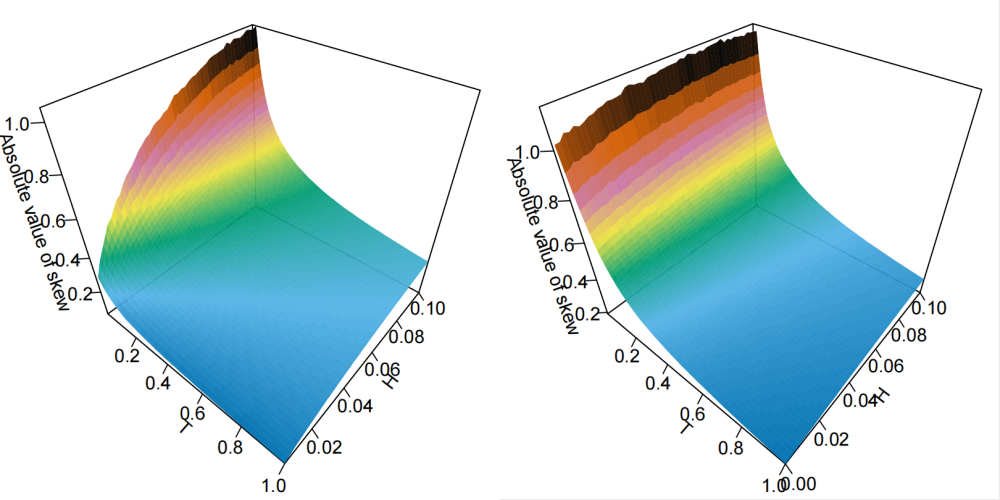
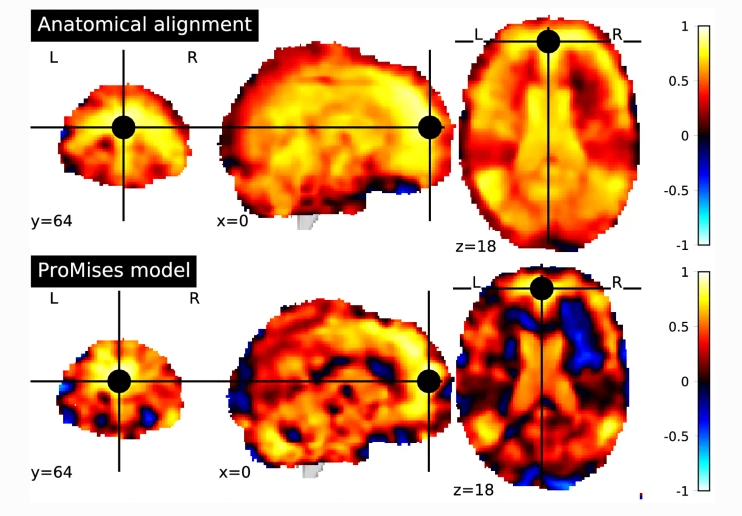
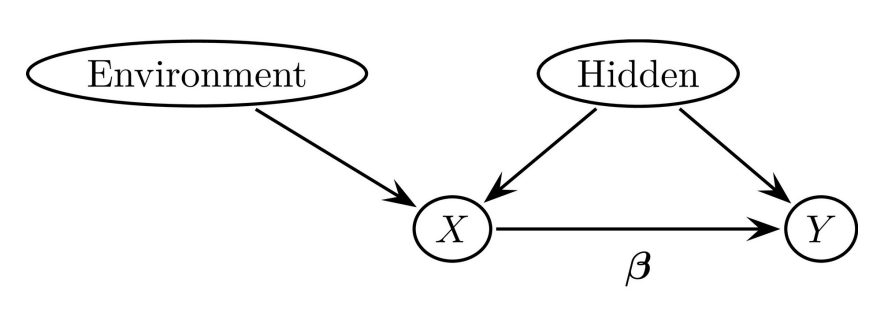
In this document, ...