Deep Learning from first principles in Python, R and Octave – Part 5
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
Introduction
a. A robot may not injure a human being or, through inaction, allow a human being to come to harm.
b. A robot must obey orders given it by human beings except where such orders would conflict with the First Law.
c. A robot must protect its own existence as long as such protection does not conflict with the First or Second Law.
Isaac Asimov's Three Laws of Robotics
Any sufficiently advanced technology is indistinguishable from magic.
Arthur C Clarke.
In this 5th part on Deep Learning from first Principles in Python, R and Octave, I solve the MNIST data set of handwritten digits (shown below), from the basics. To do this, I construct a L-Layer, vectorized Deep Learning implementation in Python, R and Octave from scratch and classify the MNIST data set. The MNIST training data set contains 60000 handwritten digits from 0-9, and a test set of 10000 digits. MNIST, is a popular dataset for running Deep Learning tests, and has been rightfully termed as the ‘drosophila’ of Deep Learning, by none other than the venerable Prof Geoffrey Hinton.

The ‘Deep Learning from first principles in Python, R and Octave’ series, so far included Part 1 , where I had implemented logistic regression as a simple Neural Network. Part 2 implemented the most elementary neural network with 1 hidden layer, but with any number of activation units in that layer, and a sigmoid activation at the output layer.
This post, ‘Deep Learning from first principles in Python, R and Octave – Part 5’ largely builds upon Part3. in which I implemented a multi-layer Deep Learning network, with an arbitrary number of hidden layers and activation units per hidden layer and with the output layer was based on the sigmoid unit, for binary classification. In Part 4, I derive the Jacobian of a Softmax, the Cross entropy loss and the gradient equations for a multi-class Softmax classifier. I also implement a simple Neural Network using Softmax classifications in Python, R and Octave.
In this post I combine Part 3 and Part 4 to to build a L-layer Deep Learning network, with arbitrary number of hidden layers and hidden units, which can do both binary (sigmoid) and multi-class (softmax) classification.
The generic, vectorized L-Layer Deep Learning Network implementations in Python, R and Octave can be cloned/downloaded from GitHub at DeepLearning-Part5. This implementation allows for arbitrary number of hidden layers and hidden layer units. The activation function at the hidden layers can be one of sigmoid, relu and tanh (will be adding leaky relu soon). The output activation can be used for binary classification with the ‘sigmoid’, or multi-class classification with ‘softmax’. Feel free to download and play around with the code!
I thought the exercise of combining the two parts(Part 3, & Part 4) would be a breeze. But it was anything but. Incorporating a Softmax classifier into the generic L-Layer Deep Learning model was a challenge. Moreover I found that I could not use the gradient descent on 60,000 training samples as my laptop ran out of memory. So I had to implement Stochastic Gradient Descent (SGD) for Python, R and Octave. In addition, I had to also implement the numerically stable version of Softmax, as the softmax and its derivative would result in NaNs.
Numerically stable Softmax
The Softmax function can be numerically unstable because of the division of large exponentials. To handle this problem we have to implement stable Softmax function as below
Therefore
Here ‘D’ can be anything. A common choice is
Here is the stable Softmax implementation in Python
# A numerically stable Softmax implementation
def stableSoftmax(Z):
#Compute the softmax of vector x in a numerically stable way.
shiftZ = Z.T - np.max(Z.T,axis=1).reshape(-1,1)
exp_scores = np.exp(shiftZ)
# normalize them for each example
A = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
cache=Z
return A,cache
While trying to create a L-Layer generic Deep Learning network in the 3 languages, I found it useful to ensure that the model executed correctly on smaller datasets. You can run into numerous problems while setting up the matrices, which becomes extremely difficult to debug. So in this post, I run the model on 2 smaller data for sets used in my earlier posts(Part 3 & Part4) , in each of the languages, before running the generic model on MNIST.
Here is a fair warning. if you think you can dive directly into Deep Learning, with just some basic knowledge of Machine Learning, you are bound to run into serious issues. Moreover, your knowledge will be incomplete. It is essential that you have a good grasp of Machine and Statistical Learning, the different algorithms, the measures and metrics for selecting the models etc.It would help to be conversant with all the ML models, ML concepts, validation techniques, classification measures etc. Check out the internet/books for background.
Incidentally you could also check out my book, Practical Machine Learning in R and Python – Machine Learning in Stereo, available on Amazon. In this book, I implement different ML algorithms, regularization techniques, model selection, ensemble methods, key measures and metrics. My book is compact, minimalist and includes implementations of many ML algorithms in R and Python, and can be used as a handy reference.

1. Random dataset with Sigmoid activation – Python
This random data with 9 clusters, was used in my post Deep Learning from first principles in Python, R and Octave – Part 3 , and was used to test the complete L-layer Deep Learning network with Sigmoid activation.
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import make_classification, make_blobs
exec(open("DLfunctions51.py").read()) # Cannot import in Rmd.
# Create a random data set with 9 centeres
X1, Y1 = make_blobs(n_samples = 400, n_features = 2, centers = 9,cluster_std = 1.3, random_state =4)
#Create 2 classes
Y1=Y1.reshape(400,1)
Y1 = Y1 % 2
X2=X1.T
Y2=Y1.T
# Set the dimensions of L -layer DL network
layersDimensions = [2, 9, 9,1] # 4-layer model
# Execute DL network with hidden activation=relu and sigmoid output function
parameters = L_Layer_DeepModel(X2, Y2, layersDimensions, hiddenActivationFunc='relu', outputActivationFunc="sigmoid",learningRate = 0.3,num_iterations = 2500, print_cost = True)
2. Spiral dataset with Softmax activation – Python
The Spiral data was used in my post Deep Learning from first principles in Python, R and Octave – Part 4 and was used to test the complete L-layer Deep Learning network with multi-class Softmax activation at the output layer
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import make_classification, make_blobs
exec(open("DLfunctions51.py").read())
# Create an input data set - Taken from CS231n Convolutional Neural networks
# http://cs231n.github.io/neural-networks-case-study/
N = 100 # number of points per class
D = 2 # dimensionality
K = 3 # number of classes
X = np.zeros((N*K,D)) # data matrix (each row = single example)
y = np.zeros(N*K, dtype='uint8') # class labels
for j in range(K):
ix = range(N*j,N*(j+1))
r = np.linspace(0.0,1,N) # radius
t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta
X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
y[ix] = j
X1=X.T
Y1=y.reshape(-1,1).T
numHidden=100 # No of hidden units in hidden layer
numFeats= 2 # dimensionality
numOutput = 3 # number of classes
# Set the dimensions of the layers
layersDimensions=[numFeats,numHidden,numOutput]
parameters = L_Layer_DeepModel(X1, Y1, layersDimensions, hiddenActivationFunc='relu', outputActivationFunc="softmax",learningRate = 0.6,num_iterations = 9000, print_cost = True)
## Cost after iteration 0: 1.098759
## Cost after iteration 1000: 0.112666
## Cost after iteration 2000: 0.044351
## Cost after iteration 3000: 0.027491
## Cost after iteration 4000: 0.021898
## Cost after iteration 5000: 0.019181
## Cost after iteration 6000: 0.017832
## Cost after iteration 7000: 0.017452
## Cost after iteration 8000: 0.017161
3. MNIST dataset with Softmax activation – Python
In the code below, I execute Stochastic Gradient Descent on the MNIST training data of 60000. I used a mini-batch size of 1000. Python takes about 40 minutes to crunch the data. In addition I also compute the Confusion Matrix and other metrics like Accuracy, Precision and Recall for the MNIST data set. I get an accuracy of 0.93 on the MNIST test set. This accuracy can be improved by choosing more hidden layers or more hidden units and possibly also tweaking the learning rate and the number of epochs.
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import pandas as pd
import math
from sklearn.datasets import make_classification, make_blobs
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
exec(open("DLfunctions51.py").read())
exec(open("load_mnist.py").read())
# Read the MNIST training and test sets
training=list(read(dataset='training',path=".\\mnist"))
test=list(read(dataset='testing',path=".\\mnist"))
# Create labels and pixel arrays
lbls=[]
pxls=[]
print(len(training))
#for i in range(len(training)):
for i in range(60000):
l,p=training[i]
lbls.append(l)
pxls.append(p)
labels= np.array(lbls)
pixels=np.array(pxls)
y=labels.reshape(-1,1)
X=pixels.reshape(pixels.shape[0],-1)
X1=X.T
Y1=y.T
# Set the dimensions of the layers. The MNIST data is 28x28 pixels= 784
# Hence input layer is 784. For the 10 digits the Softmax classifier
# has to handle 10 outputs
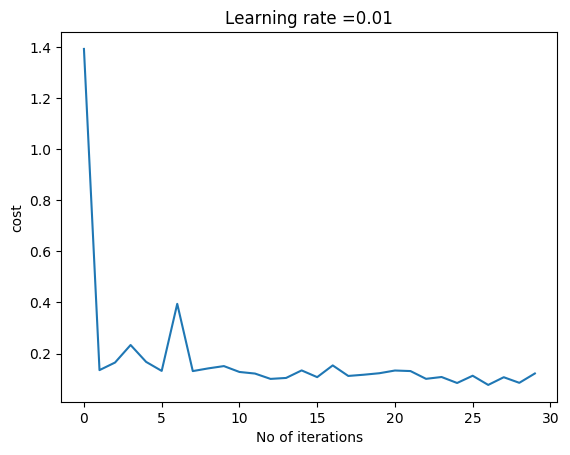
layersDimensions=[784, 15,9,10] # Works very well,lr=0.01,mini_batch =1000, total=20000
np.random.seed(1)
costs = []
# Run Stochastic Gradient Descent with Learning Rate=0.01, mini batch size=1000
# number of epochs=3000
parameters = L_Layer_DeepModel_SGD(X1, Y1, layersDimensions, hiddenActivationFunc='relu', outputActivationFunc="softmax",learningRate = 0.01 ,mini_batch_size =1000, num_epochs = 3000, print_cost = True)
# Compute the Confusion Matrix on Training set
# Compute the training accuracy, precision and recall
proba=predict_proba(parameters, X1,outputActivationFunc="softmax")
#A2, cache = forwardPropagationDeep(X1, parameters)
#proba=np.argmax(A2, axis=0).reshape(-1,1)
a=confusion_matrix(Y1.T,proba)
print(a)
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
print('Accuracy: {:.2f}'.format(accuracy_score(Y1.T, proba)))
print('Precision: {:.2f}'.format(precision_score(Y1.T, proba,average="micro")))
print('Recall: {:.2f}'.format(recall_score(Y1.T, proba,average="micro")))
# Read the test data
lbls=[]
pxls=[]
print(len(test))
for i in range(10000):
l,p=test[i]
lbls.append(l)
pxls.append(p)
testLabels= np.array(lbls)
testPixels=np.array(pxls)
ytest=testLabels.reshape(-1,1)
Xtest=testPixels.reshape(testPixels.shape[0],-1)
X1test=Xtest.T
Y1test=ytest.T
# Compute the Confusion Matrix on Test set
# Compute the test accuracy, precision and recall
probaTest=predict_proba(parameters, X1test,outputActivationFunc="softmax")
#A2, cache = forwardPropagationDeep(X1, parameters)
#proba=np.argmax(A2, axis=0).reshape(-1,1)
a=confusion_matrix(Y1test.T,probaTest)
print(a)
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
print('Accuracy: {:.2f}'.format(accuracy_score(Y1test.T, probaTest)))
print('Precision: {:.2f}'.format(precision_score(Y1test.T, probaTest,average="micro")))
print('Recall: {:.2f}'.format(recall_score(Y1test.T, probaTest,average="micro")))
##1. Confusion Matrix of Training set
0 1 2 3 4 5 6 7 8 9
## [[5854 0 19 2 10 7 0 1 24 6]
## [ 1 6659 30 10 5 3 0 14 20 0]
## [ 20 24 5805 18 6 11 2 32 37 3]
## [ 5 4 175 5783 1 27 1 58 60 17]
## [ 1 21 9 0 5780 0 5 2 12 12]
## [ 29 9 21 224 6 4824 18 17 245 28]
## [ 5 4 22 1 32 12 5799 0 43 0]
## [ 3 13 148 154 18 3 0 5883 4 39]
## [ 11 34 30 21 13 16 4 7 5703 12]
## [ 10 4 1 32 135 14 1 92 134 5526]]
##2. Accuracy, Precision, Recall of Training set
## Accuracy: 0.96
## Precision: 0.96
## Recall: 0.96
##3. Confusion Matrix of Test set
0 1 2 3 4 5 6 7 8 9
## [[ 954 1 8 0 3 3 2 4 4 1]
## [ 0 1107 6 5 0 0 1 2 14 0]
## [ 11 7 957 10 5 0 5 20 16 1]
## [ 2 3 37 925 3 13 0 8 18 1]
## [ 2 6 1 1 944 0 7 3 4 14]
## [ 12 5 4 45 2 740 24 8 42 10]
## [ 8 4 4 2 16 9 903 0 12 0]
## [ 4 10 27 18 5 1 0 940 1 22]
## [ 11 13 6 13 9 10 7 2 900 3]
## [ 8 5 1 7 50 7 0 20 29 882]]
##4. Accuracy, Precision, Recall of Training set
## Accuracy: 0.93
## Precision: 0.93
## Recall: 0.93
4. Random dataset with Sigmoid activation – R code
This is the random data set used in the Python code above which was saved as a CSV. The code is used to test a L -Layer DL network with Sigmoid Activation in R.
source("DLfunctions5.R")
# Read the random data set
z <- as.matrix(read.csv("data.csv",header=FALSE))
x <- z[,1:2]
y <- z[,3]
X <- t(x)
Y <- t(y)
# Set the dimensions of the layer
layersDimensions = c(2, 9, 9,1)
# Run Gradient Descent on the data set with relu hidden unit activation
# sigmoid activation unit in the output layer
retvals = L_Layer_DeepModel(X, Y, layersDimensions,
hiddenActivationFunc='relu',
outputActivationFunc="sigmoid",
learningRate = 0.3,
numIterations = 5000,
print_cost = True)
#Plot the cost vs iterations
iterations <- seq(0,5000,1000)
costs=retvals$costs
df=data.frame(iterations,costs)
ggplot(df,aes(x=iterations,y=costs)) + geom_point() + geom_line(color="blue") +
ggtitle("Costs vs iterations") + xlab("Iterations") + ylab("Loss")
5. Spiral dataset with Softmax activation – R
The spiral data set used in the Python code above, is reused to test multi-class classification with Softmax.
source("DLfunctions5.R")
Z <- as.matrix(read.csv("spiral.csv",header=FALSE))
# Setup the data
X <- Z[,1:2]
y <- Z[,3]
X <- t(X)
Y <- t(y)
# Initialize number of features, number of hidden units in hidden layer and
# number of classes
numFeats<-2 # No features
numHidden<-100 # No of hidden units
numOutput<-3 # No of classes
# Set the layer dimensions
layersDimensions = c(numFeats,numHidden,numOutput)
# Perform gradient descent with relu activation unit for hidden layer
# and softmax activation in the output
retvals = L_Layer_DeepModel(X, Y, layersDimensions,
hiddenActivationFunc='relu',
outputActivationFunc="softmax",
learningRate = 0.5,
numIterations = 9000,
print_cost = True)
#Plot cost vs iterations
iterations <- seq(0,9000,1000)
costs=retvals$costs
df=data.frame(iterations,costs)
ggplot(df,aes(x=iterations,y=costs)) + geom_point() + geom_line(color="blue") +
ggtitle("Costs vs iterations") + xlab("Iterations") + ylab("Costs")
6. MNIST dataset with Softmax activation – R
The code below executes a L – Layer Deep Learning network with Softmax output activation, to classify the 10 handwritten digits from MNIST with Stochastic Gradient Descent. The entire 60000 data set was used to train the data. R takes almost 8 hours to process this data set with a mini-batch size of 1000. The use of ‘for’ loops is limited to iterating through epochs, mini batches and for creating the mini batches itself. All other code is vectorized. Yet, it seems to crawl. Most likely the use of ‘lists’ in R, to return multiple values is performance intensive. Some day, I will try to profile the code, and see where the issue is. However the code works!
Having said that, the Confusion Matrix in R dumps a lot of interesting statistics! There is a bunch of statistical measures for each class. For e.g. the Balanced Accuracy for the digits ‘6’ and ‘9’ is around 50%. Looks like, the classifier is confused by the fact that 6 is inverted 9 and vice-versa. The accuracy on the Test data set is just around 75%. I could have played around with the number of layers, number of hidden units, learning rates, epochs etc to get a much higher accuracy. But since each test took about 8+ hours, I may work on this, some other day!
source("DLfunctions5.R")
source("mnist.R")
#Load the mnist data
load_mnist()
show_digit(train$x[2,])
#Set the layer dimensions
layersDimensions=c(784, 15,9, 10) # Works at 1500
x <- t(train$x)
X <- x[,1:60000]
y <-train$y
y1 <- y[1:60000]
y2 <- as.matrix(y1)
Y=t(y2)
# Execute Stochastic Gradient Descent on the entire training set
# with Softmax activation
retvalsSGD= L_Layer_DeepModel_SGD(X, Y, layersDimensions,
hiddenActivationFunc='relu',
outputActivationFunc="softmax",
learningRate = 0.01,
mini_batch_size = 1000,
num_epochs = 1,
print_cost = True)

# Compute the Confusion Matrix
library(caret)
library(e1071)
predictions=predictProba(retvalsSGD[['parameters']], X,hiddenActivationFunc='relu',
outputActivationFunc="softmax")
confusionMatrix(predictions,Y)
# Confusion Matrix on the Training set
> confusionMatrix(predictions,Y)
Confusion Matrix and Statistics
Reference
Prediction 0 1 2 3 4 5 6 7 8 9
0 5738 1 21 5 16 17 7 15 9 43
1 5 6632 21 24 25 3 2 33 13 392
2 12 32 5747 106 25 28 3 27 44 4779
3 0 27 12 5715 1 21 1 20 1 13
4 10 5 21 18 5677 9 17 30 15 166
5 142 21 96 136 93 5306 5884 43 60 413
6 0 0 0 0 0 0 0 0 0 0
7 6 9 13 13 3 4 0 6085 0 55
8 8 12 7 43 1 32 2 7 5703 69
9 2 3 20 71 1 1 2 5 6 19
Overall Statistics
Accuracy : 0.777
95% CI : (0.7737, 0.7804)
No Information Rate : 0.1124
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.7524
Mcnemar's Test P-Value : NA
Statistics by Class:
Class: 0 Class: 1 Class: 2 Class: 3 Class: 4 Class: 5 Class: 6
Sensitivity 0.96877 0.9837 0.96459 0.93215 0.97176 0.97879 0.00000
Specificity 0.99752 0.9903 0.90644 0.99822 0.99463 0.87380 1.00000
Pos Pred Value 0.97718 0.9276 0.53198 0.98348 0.95124 0.43513 NaN
Neg Pred Value 0.99658 0.9979 0.99571 0.99232 0.99695 0.99759 0.90137
Prevalence 0.09872 0.1124 0.09930 0.10218 0.09737 0.09035 0.09863
Detection Rate 0.09563 0.1105 0.09578 0.09525 0.09462 0.08843 0.00000
Detection Prevalence 0.09787 0.1192 0.18005 0.09685 0.09947 0.20323 0.00000
Balanced Accuracy 0.98314 0.9870 0.93551 0.96518 0.98319 0.92629 0.50000
Class: 7 Class: 8 Class: 9
Sensitivity 0.9713 0.97471 0.0031938
Specificity 0.9981 0.99666 0.9979464
Pos Pred Value 0.9834 0.96924 0.1461538
Neg Pred Value 0.9967 0.99727 0.9009521
Prevalence 0.1044 0.09752 0.0991500
Detection Rate 0.1014 0.09505 0.0003167
Detection Prevalence 0.1031 0.09807 0.0021667
Balanced Accuracy 0.9847 0.98568 0.5005701
# Confusion Matrix on the Training set xtest <- t(test$x) Xtest <- xtest[,1:10000] ytest <-test$y ytest1 <- ytest[1:10000] ytest2 <- as.matrix(ytest1) Ytest=t(ytest2)
Confusion Matrix and Statistics
Reference
Prediction 0 1 2 3 4 5 6 7 8 9
0 950 2 2 3 0 6 9 4 7 6
1 3 1110 4 2 9 0 3 12 5 74
2 2 6 965 21 9 14 5 16 12 789
3 1 2 9 908 2 16 0 21 2 6
4 0 1 9 5 938 1 8 6 8 39
5 19 5 25 35 20 835 929 8 54 67
6 0 0 0 0 0 0 0 0 0 0
7 4 4 7 10 2 4 0 952 5 6
8 1 5 8 14 2 16 2 3 876 21
9 0 0 3 12 0 0 2 6 5 1
Overall Statistics
Accuracy : 0.7535
95% CI : (0.7449, 0.7619)
No Information Rate : 0.1135
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.7262
Mcnemar's Test P-Value : NA
Statistics by Class:
Class: 0 Class: 1 Class: 2 Class: 3 Class: 4 Class: 5 Class: 6
Sensitivity 0.9694 0.9780 0.9351 0.8990 0.9552 0.9361 0.0000
Specificity 0.9957 0.9874 0.9025 0.9934 0.9915 0.8724 1.0000
Pos Pred Value 0.9606 0.9083 0.5247 0.9390 0.9241 0.4181 NaN
Neg Pred Value 0.9967 0.9972 0.9918 0.9887 0.9951 0.9929 0.9042
Prevalence 0.0980 0.1135 0.1032 0.1010 0.0982 0.0892 0.0958
Detection Rate 0.0950 0.1110 0.0965 0.0908 0.0938 0.0835 0.0000
Detection Prevalence 0.0989 0.1222 0.1839 0.0967 0.1015 0.1997 0.0000
Balanced Accuracy 0.9825 0.9827 0.9188 0.9462 0.9733 0.9043 0.5000
Class: 7 Class: 8 Class: 9
Sensitivity 0.9261 0.8994 0.0009911
Specificity 0.9953 0.9920 0.9968858
Pos Pred Value 0.9577 0.9241 0.0344828
Neg Pred Value 0.9916 0.9892 0.8989068
Prevalence 0.1028 0.0974 0.1009000
Detection Rate 0.0952 0.0876 0.0001000
Detection Prevalence 0.0994 0.0948 0.0029000
Balanced Accuracy 0.9607 0.9457 0.4989384
7. Random dataset with Sigmoid activation – Octave
The Octave code below uses the random data set used by Python. The code below implements a L-Layer Deep Learning with Sigmoid Activation.
source("DL5functions.m")
# Read the data
data=csvread("data.csv");
X=data(:,1:2);
Y=data(:,3);
#Set the layer dimensions
layersDimensions = [2 9 7 1]; #tanh=-0.5(ok), #relu=0.1 best!
# Perform gradient descent
[weights biases costs]=L_Layer_DeepModel(X', Y', layersDimensions,
hiddenActivationFunc='relu',
outputActivationFunc="sigmoid",
learningRate = 0.1,
numIterations = 10000);
# Plot cost vs iterations
plotCostVsIterations(10000,costs);

8. Spiral dataset with Softmax activation – Octave
The code below uses the spiral data set used by Python above. The code below implements a L-Layer Deep Learning with Softmax Activation.
# Read the data
data=csvread("spiral.csv");
# Setup the data
X=data(:,1:2);
Y=data(:,3);
# Set the number of features, number of hidden units in hidden layer and number of classess
numFeats=2; #No features
numHidden=100; # No of hidden units
numOutput=3; # No of classes
# Set the layer dimensions
layersDimensions = [numFeats numHidden numOutput];
#Perform gradient descent with softmax activation unit
[weights biases costs]=L_Layer_DeepModel(X', Y', layersDimensions,
hiddenActivationFunc='relu',
outputActivationFunc="softmax",
learningRate = 0.1,
numIterations = 10000);

9. MNIST dataset with Softmax activation – Octave
The code below implements a L-Layer Deep Learning Network in Octave with Softmax output activation unit, for classifying the 10 handwritten digits in the MNIST dataset. Unfortunately, Octave can only index to around 10000 training at a time, and I was getting an error ‘error: out of memory or dimension too large for Octave’s index type error: called from…’, when I tried to create a batch size of 20000. So I had to come with a work around to create a batch size of 10000 (randomly) and then use a mini-batch of 1000 samples and execute Stochastic Gradient Descent. The performance was good. Octave takes about 15 minutes, on a batch size of 10000 and a mini batch of 1000.
I thought if the performance was not good, I could iterate through these random batches and refining the gradients as follows
# Pseudo code that could be used since Octave only allows 10K batches
# at a time
# Randomly create weights
[weights biases] = initialize_weights()
for i=1:k
# Create a random permutation and create a random batch
permutation = randperm(10000);
X=trainX(permutation,:);
Y=trainY(permutation,:);
# Compute weights from SGD and update weights in the next batch update
[weights biases costs]=L_Layer_DeepModel_SGD(X,Y,mini_bactch=1000,weights, biases,...);
...
endfor
# Load the MNIST data
load('./mnist/mnist.txt.gz');
#Create a random permutatation from 60K
permutation = randperm(10000);
disp(length(permutation));
# Use this 10K as the batch
X=trainX(permutation,:);
Y=trainY(permutation,:);
# Set layer dimensions
layersDimensions=[784, 15, 9, 10];
# Run Stochastic Gradient descent with batch size=10K and mini_batch_size=1000
[weights biases costs]=L_Layer_DeepModel_SGD(X', Y', layersDimensions,
hiddenActivationFunc='relu',
outputActivationFunc="softmax",
learningRate = 0.01,
mini_batch_size = 2000, num_epochs = 5000);

9. Final thoughts
Here are some of my final thoughts after working on Python, R and Octave in this series and in other projects
1. Python, with its highly optimized numpy library, is ideally suited for creating Deep Learning Models, which have a lot of matrix manipulations. Python is a real workhorse when it comes to Deep Learning computations.
2. R is somewhat clunky in comparison to its cousin Python in handling matrices or in returning multiple values. But R’s statistical libraries, dplyr, and ggplot are really superior to the Python peers. Also, I find R handles dataframes, much better than Python.
3. Octave is a no-nonsense,minimalist language which is very efficient in handling matrices. It is ideally suited for implementing Machine Learning and Deep Learning from scratch. But Octave has its problems and cannot handle large matrix sizes, and also lacks the statistical libaries of R and Python. They possibly exist in its sibling, Matlab
Feel free to clone/download the code from GitHub at DeepLearning-Part5.
Conclusion
Building a Deep Learning Network from scratch is quite challenging, time-consuming but nevertheless an exciting task. While the statements in the different languages for manipulating matrices, summing up columns, finding columns which have ones don’t take more than a single statement, extreme care has to be taken to ensure that the statements work well for any dimension. The lessons learnt from creating L -Layer Deep Learning network are many and well worth it. Give it a try!
Hasta la vista! I’ll be back, so stick around!
Watch this space!
References
1. Deep Learning Specialization
2. Neural Networks for Machine Learning
3. CS231 Convolutional Neural Networks for Visual Recognition
4. Eli Bendersky’s Website – The Softmax function and its derivative
Also see
1. My book ‘Practical Machine Learning with R and Python’ on Amazon
2. Presentation on Wireless Technologies – Part 1
3. Exploring Quantum Gate operations with QCSimulator
4. What’s up Watson? Using IBM Watson’s QAAPI with Bluemix, NodeExpress – Part 1
5. TWS-4: Gossip protocol: Epidemics and rumors to the rescue
6. cricketr plays the ODIs!
7. “Is it an animal? Is it an insect?” in Android
8. The 3rd paperback & kindle editions of my books on Cricket, now on Amazon
9. Deblurring with OpenCV: Weiner filter reloaded
10. GooglyPlus: yorkr analyzes IPL players, teams, matches with plots and tables
To see all posts click Index of Posts
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.