Introduction

Recently, I introduced the golden search method – a special way to save computation time by modifying the bisection method with the golden ratio, and I illustrated how to minimize a cusped function with this script.  I also wrote an R function to implement this method and an R script on how to apply this method with this example.  Today, I will use apply this method to a statistical topic: minimizing the sum of absolute deviations with the median.

While reading Page 148 (Section 6.3) in Michael Trosset’s “An Introduction to Statistical Inference and Its Applications”, I learned 2 basic, simple, yet interesting theorems.

If X is a random variable with a population mean and a population median , then

a) minimizes the function

b) minimizes the function

I won’t prove these theorems in this blog post (perhaps later), but I want to use the golden section search method to show a result similar to b):

c) The sample median, , minimizes the function

.

This is not surprising, of course, since

– is just a function of the random variable

– by the law of large numbers,

Thus, if the median minimizes , then, intuitively, it minimizes .  Let’s show this with the golden section search method, and let’s explore any differences that may arise between odd-numbered and even-numbered data sets.

Minimizing a Data Set with an Odd Number of Data

Consider this following data set with an odd number of data:

A = {5, 9, 11, 14, ,17}

Here is the plot of the function

for this data set.

This function is clearly cusped at multiple points and has a unique minimum.  Thus, the golden section search method is suitable for minimizing it.

To use my R script to find the minimizer, I need to

– define an R function for this above function (I call it sum.of.distances1 – see the R scripts at the bottom of this blog post)

– call both this above function and the function for the golden section search method with the source() command

– feed the 4 required arguments – objective function (sum.of.distances1), the lower and upper bounds (0, 20), and the tolerance (1e-5) – to golden.section.search()

Here is the output after the first iteration:

Iteration # 1 
f1 = 23.08204 
f2 = 18.36068 
f2 < f1 
New Upper Bound = 20 
New Lower Bound = 7.63932 
New Lower Test Point =  12.36068 
New Upper Test Point =  15.27864

Here is the output after the final iteration, including the resulting minimizer:

Iteration # 31 
f1 = 17 
f2 = 17 
f2 > f1 
New Upper Bound = 11 
New Lower Bound = 11 
New Upper Test Point =  11 
New Lower Test Point =  11 
Final Lower Bound = 11 
Final Upper Bound = 11 
Estimated Minimizer = 11

This is, of course, the median of A = {5, 9, 11, 14, ,17}.  You can confirm it in R by using the median() function:

data.vector1 = c(5, 9, 11, 14, 17)
median(data.vector1)

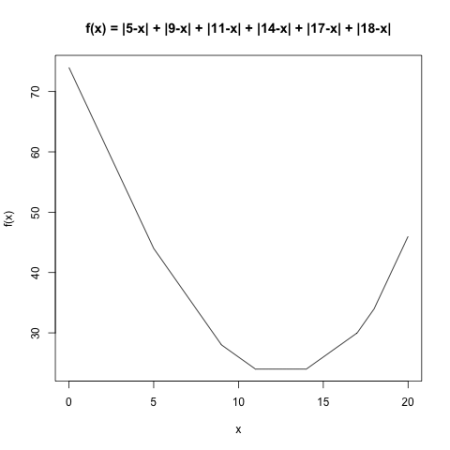
Minimizing a Data Set with an Even Number of Data

Now, what about a data set with an even number of data?

B = {5, 9, 11, 14, ,17, 18}

Here is the plot of the objective function.

Notice that, between and , the function is horizontal line.  This makes intuitive sense; if you think back to learning how to calculate the median of a data set with an even number of data, the median is NOT one of the data, but an interpolated value between the 2 “middle” data (the average of the 2 “middle” data is usually used).  You can confirm this interpolation with the median() function in R.

data.vector2 = c(5, 9, 11, 14, 17, 18)
median(data.vector2)

For a data set with an even number of data, interpolation is needed because there is no unique number such that there are equal number of data larger and smaller than itself.

This non-uniqueness of the median is reflected in the minimization with the golden section search method.  The minimizer varies depending on the initial lower and upper bounds.

- If I use 0 and 20 as the initial lower and upper bounds, here is the output of the final iteration and the resulting minimizer.

Iteration # 31 
f1 = 24 
f2 = 24 
f2 < f1 
New Upper Bound = 13.74744 
New Lower Bound = 13.74743 
New Lower Test Point =  13.74743 
New Upper Test Point =  13.74743 
Final Lower Bound = 13.74743 
Final Upper Bound = 13.74744 
Estimated Minimizer = 13.74743

- If I use 1 and 20 as the initial lower and upper bounds instead, here is the corresponding output.

Iteration # 31 
f1 = 24 
f2 = 24 
f2 < f1 
New Upper Bound = 13.80178 
New Lower Bound = 13.80177 
New Lower Test Point =  13.80178 
New Upper Test Point =  13.80178 
Final Lower Bound = 13.80177 
Final Upper Bound = 13.80178 
Estimated Minimizer = 13.80178

Summary

Thus, the lessons to be taken away from this exercise are:

1) The median minimizes the function

2) There is a unique median for a data set with an odd number of data, but there is no unique median for a data set with an even number of data.

Reference

This blog post was inspired by Exercise #2 in Section 7.1 on Page 135 in “A First Course in Statistical Programming with R” by John Braun and Duncan Murdoch.

R Script

I saved the 2 objective functions in a file called sum.of.distances.R:

# odd number of data
sum.of.distances1 = function(x)
{
     abs(5-x) + abs(9-x) + abs(11-x) + abs(14-x) + abs(17-x)
}

# even number of data
sum.of.distances2 = function(x)
{
     abs(5-x) + abs(9-x) + abs(11-x) + abs(14-x) + abs(17-x) + abs(18-x)
}

See my previous post for the function that conducts the golden section search.  In a separate script called “minimization.R”, I ran the following:

##### Showing that the median minimizes the sum of absolute deviations
##### By Eric Cai - The Chemical Statistician
source('sum.of.distances.R')
png('INSERT YOUR DIRECTORY PATH HERE/example data 1.png')
curve(sum.of.distances1, from = 0, to = 20, main = 'f(x) = |5-x| + |9-x| + |11-x| + |14-x| + |17-x|', ylab = 'f(x)')
dev.off()

golden.section.search(sum.of.distances1, 0, 20, 1e-5) 

data.vector1 = c(5, 9, 11, 14, 17)
median(data.vector1)

png('INSERT YOUR DIRECTORY PATH HERE/example data 2.png') 
curve(sum.of.distances2, from = 0, to = 20, main = 'f(x) = |5-x| + |9-x| + |11-x| + |14-x| + |17-x| + |18-x|', ylab = 'f(x)') 
dev.off() 

golden.section.search(sum.of.distances2, 0, 20, 1e-5) 
golden.section.search(sum.of.distances2, 1, 20, 1e-5) 

data.vector2 = c(5, 9, 11, 14, 17, 18) 
median(data.vector2)