Estimating the Decay Rate and the Half-Life of DDT in Trout – Applying Simple Linear Regression with Logarithmic Transformation

Posted on March 24, 2013 by Eric Cai - The Chemical Statistician in R bloggers | 0 Comments

[This article was first published on The Chemical Statistician » R programming, and kindly contributed to R-bloggers]. (You can report issue about the content on this page here)

Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.

This blog post uses a function and a script written in R that were displayed in an earlier blog post.

Introduction

This is the second of a series of blog posts about simple linear regression; the first was written recently on some conceptual nuances and subtleties about this model. In this blog post, I will use simple linear regression to analyze a data set with a logarithmic transformation and discuss how to make inferences on the regression coefficients and the means of the target on the original scale. The data document the decay of dichlorodiphenyltrichloroethane (DDT) in trout in Lake Michigan; I found it on Page 49 in the book ”Elements of Environmental Chemistry” by Ronald A. Hites. Future posts will also be written on the chemical aspects of this topic, including the environmental chemistry of DDT and exponential decay in chemistry and, in particular, radiochemistry.

Dichlorodiphenyltrichloroethane (DDT)

Source: Wikimedia Commons

A serious student of statistics or a statistician re-learning the fundamentals like myself should always try to understand the math and the statistics behind a software’s built-in function rather than treating it like a black box. This is especially worthwhile for a basic yet powerful tool like simple linear regression. Thus, instead of simply using the lm() function in R, I will reproduce the calculations done by lm() with my own function and script (posted earlier on my blog) to obtain inferential statistics on the regression coefficients. However, I will not write or explain the math behind the calculations; they are shown in my own function with very self-evident variable names, in case you are interested. The calculations are arguably the most straightforward aspects of linear regression, and you can easily find the derivations and formulas on the web, in introductory or applied statistics textbooks, and in regression textbooks.

Linearizing a Non-Linear Relationship

As I mentioned previously in my last blog post about some conceptual foundations of simple linear regression, the “linear” term in the name refers to the linearity between the target and the regression coefficients ( $\beta_0$ and $\beta_1$ ). The relationship between the target (Y) and the predictor (x) may not be linear to begin with, and some transformation may be required to linearize the predictor-target relationship. The exponential decay of an environmental pollutant is an example of such a model that can be linearized for simple linear regression to be used.

The exponential decay of a chemical’s concentration can be mathematically described as follows:

$C(t) = C_0e^{-\lambda t}$ .

– $t$ is the time

– $C_0$ is the initial concentration of the chemical

– $C(t)$ is the concentration of the chemical at time $t$

– $\lambda$ is the rate of decay

This is especially common for radioactive decay. It can be shown mathematically using differential equations that a chemical will decay exponentially if the following conditions are satisfied:

1) There is no influx of the chemical into the system in question.

2) The rate of decay (or outflux) of the chemical is proportional to its amount in the system.

If $C(t)$ is the target variable and $t$ is the predictor variable, then it is clear that the above equation is not linear between $C(t)$ and $t$ . However, let’s evaluate the natural logarithm of each side.

$ln[C(t)] = ln[C_0] - \lambda t$

If $ln[C(t)]$ is the target variable and $t$ is the predictor variable, then this is a linear relationship between the target and the predictor. $ln[C_0]$ is the y-intercept, and $\lambda$ is the rate of exponential change. The negative sign in front of $\lambda$ specifies that it $ln[C(t)]$ decreases or decays with respect to $t$ .

Linearizing the Exponential Decay Model

Here are the data that I will use to illustrate simple linear regression.

             Time (Year)      DDT Concentration
 [1,]        1970             19.19
 [2,]        1971             13.00
 [3,]        1972             11.31
 [4,]        1973              9.96
 [5,]        1974              8.42
 [6,]        1975              7.50
 [7,]        1976              5.65
 [8,]        1977              6.34
 [9,]        1978              4.58
[10,]        1979              6.91
[11,]        1980              4.74
[12,]        1981              3.22
[13,]        1982              2.74
[14,]        1984              2.22
[15,]        1986              1.10
[16,]        1988              1.44
[17,]        1990              1.39
[18,]        1992              1.16
[19,]        1995              0.98
[20,]        1998              0.85

Here is the scatter plot of these raw, untransformed data.

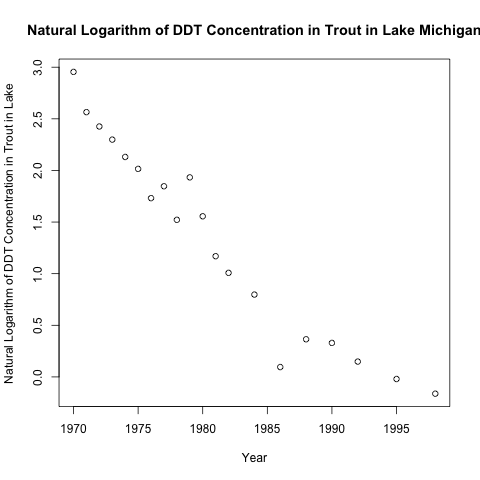
As you can see, the relationship is not very linear. Here is the scatter plot with the natural logarithmic transformation.

As expected, the relationship between the target and the predictor post-transformation looks much more linear.

My Own R Function for Simple Linear Regression

In an earlier blog post, I wrote my own function and script to conduct simple linear regression. Before I ran my script, I made sure to change my working directory to the folder containing this function, which was stored in the same folder as the script. Notice that I used the source() function to call my function, simple.linear.regression(), so that it is loaded onto the workspace first. I then ran simple.linear.regression() with my 2 vectors of the predictor and the target as the 2 arguments. You can see that I tried to replicate the 4 main columns of the output from the lm() function.

> source('simple linear regression.R')
> DDT.regression.Eric = simple.linear.regression(year, ln.DDT)
> DDT.regression.Eric
        Estimated Coefficient     Standard Error    t-statistic      p-value
beta0   225.9138462               14.308314047      15.78899         5.450466e-12
beta1   -0.1133633                0.007222532      -15.69579         6.021962e-12

Estimating the Decay Rate and the Half-Life of a Chemical from Simple Linear Regression

Recall that simple linear regression was fitted for the model

$ln[C(t)] = ln[C_0] - \lambda t$ .

From the results above, the estimate of the decay rate, $\lambda$ , is 0.1133633. (The negative sign in front of the estimate indicates that this is a decay rather than a growth.) The p-value is 6.021962e-12, so there is overwhelmingly strong evidence for this estimate to be statistically significant.

A valuable quantity for chemists to gauge the length of time that a pollutant will stay in its environment is its half-life. I see it often calculated from a single datum in textbook examples and exercises; I think that it is much better to collect many data on the concentration of the pollutant as it decays and estimate the half-life from simple linear regression to reduce noise in the estimation. To estimate the half-life, set $C(t)$ to be half of the initial concentration, $C_0$ , and solve for time.

$0.5 C_0 = C_0 e^{-0.1133633 t}$

$0.5 = e^{-0.1133633 t}$

$\frac{ln(0.5)}{-0.1133633} = t_{1/2}$

$6.114388 \ \text{Years} = t_{1/2} = \text{Half-life}$

Filed under: Applied Statistics, Environmental Chemistry, Physical Chemistry, Plots, R programming Tagged: applied statistics, data, data analysis, data visualization, DDT, exponential decay, linear regression, logarithmic transformation, plot, plots, plotting, R, R programming, regression, scatter plot, simple linear regression, statistics, transformation, transformed response, transformed target

To leave a comment for the author, please follow the link and comment on their blog: The Chemical Statistician » R programming.

R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.

Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.

R-bloggers

R news and tutorials contributed by hundreds of R bloggers

Estimating the Decay Rate and the Half-Life of DDT in Trout – Applying Simple Linear Regression with Logarithmic Transformation

Introduction

Linearizing a Non-Linear Relationship

Linearizing the Exponential Decay Model

My Own R Function for Simple Linear Regression

Estimating the Decay Rate and the Half-Life of a Chemical from Simple Linear Regression

Related

Introduction

Linearizing a Non-Linear Relationship

Linearizing the Exponential Decay Model

My Own R Function for Simple Linear Regression

Estimating the Decay Rate and the Half-Life of a Chemical from Simple Linear Regression

Related

Never miss an update! Subscribe to R-bloggers to receive e-mails with the latest R posts. (You will not see this message again.)

Never miss an update!
Subscribe to R-bloggers to receive
e-mails with the latest R posts.
(You will not see this message again.)