In the practice of risk modeling, it is sometimes mandatory to maintain a monotonic relationship between the response and each predictor. Below is a demonstration showing how to develop a generalized boosted regression with a monotonic marginal effect for each predictor.

##################################################
# FIT A GENERALIZED BOOSTED REGRESSION MODEL     #
# FOLLOWING FRIEDMAN'S GRADIENT BOOSTING MACHINE #
##################################################

library(gbm)
data1 <- read.table("/home/liuwensui/Documents/data/credit_count.txt", header = TRUE, sep = ",")
data2 <- data1[data1$CARDHLDR == 1, -1]

# Calculate the Correlation Direction Between Response and Predictors
mono <- cor(data2[, 1], data2[, -1], method = 'spearman') / abs(cor(data2[, 1], data2[, -1], method = 'spearman'))

# Train a Generalized Boosted Regression
set.seed(2012)
m <- gbm(BAD ~ ., data = data2, var.monotone = mono, distribution = "bernoulli", n.trees = 1000, shrinkage = 0.01,
         interaction.depth = 1, bag.fraction = 0.5, train.fraction = 0.8, cv.folds = 5, verbose = FALSE)

# Return the Optimal # of Iterations
best.iter <- gbm.perf(m, method = "cv", plot.it = FALSE)
print(best.iter)

# Calculate Variable Importance
imp <- summary(m, n.trees = best.iter, plotit = FALSE)

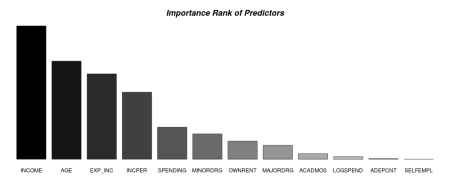
# Plot Variable Importance
png('/home/liuwensui/Documents/code/imp.png', width = 1000, height = 400)
par(mar = c(3, 0, 4, 0))
barplot(imp[, 2], col = gray(0:(ncol(data2) - 1) / (ncol(data2) - 1)),
        names.arg = imp[, 1], yaxt = "n", cex.names = 1);
title(main = list("Importance Rank of Predictors", font = 4, cex = 1.5));
dev.off()

# Plot Marginal Effects of Predictors
png('/home/liuwensui/Documents/code/mareff.png', width = 1000, height = 1000)
par(mfrow = c(3, 4), mar = c(1, 1, 1, 1), pty = "s")
for (i in 1:(ncol(data2) - 1))
  {
    plot.gbm(m, i, best.iter);
    rug(data2[, i + 1])
  }
dev.off()

Plot of Variable Importance

Plot of Monotonic Marginal Effects