Call:
lm(formula = y1 ~ x1)
 
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept)   3.0001     1.1247   2.667  0.02573 *
x1            0.5001     0.1179   4.241  0.00217 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
Residual standard error: 1.237 on 9 degrees of freedom
Multiple R-squared: 0.6665,	Adjusted R-squared: 0.6295
F-statistic: 17.99 on 1 and 9 DF,  p-value: 0.00217 

> data(anscombe)
> reg1=lm(y1~x1,data=anscombe)

Can we say something if we look (only) at that output ? The intercept is significatively non-null, as well as the slope, the 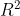 is large (66%). It looks like we do have a nice model here. And in a perfect world, we might hope that data are coming from this kind of dataset, 

But it might be possible to have completely different kinds of patterns. Actually, four differents sets of data are coming from Anscombe (1973). And that all those datasets are somehow equivalent: the 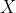‘s have the same mean, and the same variance

> apply(anscombe[,1:4],2,mean)
x1 x2 x3 x4
9  9  9  9
> apply(anscombe[,1:4],2,var)
x1 x2 x3 x4
11 11 11 11 

and so are the 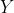‘s

> apply(anscombe[,5:8],2,mean)
y1       y2       y3       y4
7.500909 7.500909 7.500000 7.500909
> apply(anscombe[,5:8],2,var)
y1       y2       y3       y4
4.127269 4.127629 4.122620 4.123249 

Further, observe also that the correlation between the 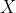‘s and the 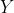‘s is the same

> cor(anscombe)[1:4,5:8]
y1         y2         y3         y4
x1  0.8164205  0.8162365  0.8162867 -0.3140467
x2  0.8164205  0.8162365  0.8162867 -0.3140467
x3  0.8164205  0.8162365  0.8162867 -0.3140467
x4 -0.5290927 -0.7184365 -0.3446610  0.8165214
> diag(cor(anscombe)[1:4,5:8])
[1] 0.8164205 0.8162365 0.8162867 0.8165214

which yields the same regression line (intercept and slope)

> cbind(coef(reg1),coef(reg2),coef(reg3),coef(reg4))
[,1]     [,2]      [,3]      [,4]
(Intercept) 3.0000909 3.000909 3.0024545 3.0017273
x1          0.5000909 0.500000 0.4997273 0.4999091

But there is more. Much more. For instance, we always have the standard deviation for residuals

> c(summary(reg1)$sigma,summary(reg2)$sigma,
+ summary(reg3)$sigma,summary(reg4)$sigma)
[1] 1.236603 1.237214 1.236311 1.235695

Thus, all regressions here have the same R2

> c(summary(reg1)$r.squared,summary(reg2)$r.squared,
+ summary(reg3)$r.squared,summary(reg4)$r.squared)
[1] 0.6665425 0.6662420 0.6663240 0.6667073

Finally, Fisher’s F statistics is also (almost) the same.

+ c(summary(reg1)$fstatistic[1],summary(reg2)$fstatistic[1],
+ summary(reg3)$fstatistic[1],summary(reg4)$fstatistic[1])
value    value    value    value
17.98994 17.96565 17.97228 18.00329 

Thus, with the following datasets, we have the same prediction (and the same confidence intervals). Consider for instance the second dataset (the first one being mentioned above),

> reg2=lm(y2~x2,data=anscombe)

The output is here exactly the same as the one we had above

> summary(reg2)
 
Call:
lm(formula = y2 ~ x2, data = anscombe)
 
Residuals:
Min      1Q  Median      3Q     Max
-1.9009 -0.7609  0.1291  0.9491  1.2691
 
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept)    3.001      1.125   2.667  0.02576 *
x2             0.500      0.118   4.239  0.00218 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
Residual standard error: 1.237 on 9 degrees of freedom
Multiple R-squared: 0.6662,	Adjusted R-squared: 0.6292
F-statistic: 17.97 on 1 and 9 DF,  p-value: 0.002179 

Here, the perfect model is the one obtained with a quadratic regression.

> reg2b=lm(y2~x2+I(x2^2),data=anscombe)
> summary(reg2b)
 
Call:
lm(formula = y2 ~ x2 + I(x2^2), data = anscombe)
 
Residuals:
Min         1Q     Median         3Q        Max
-0.0013287 -0.0011888 -0.0006294  0.0008741  0.0023776
 
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -5.9957343  0.0043299   -1385   <2e-16 ***
x2           2.7808392  0.0010401    2674   <2e-16 ***
I(x2^2)     -0.1267133  0.0000571   -2219   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
Residual standard error: 0.001672 on 8 degrees of freedom
Multiple R-squared:     1,	Adjusted R-squared:     1
F-statistic: 7.378e+06 on 2 and 8 DF,  p-value: < 2.2e-16 

> reg3=lm(y3~x3,data=anscombe)

> summary(reg3)
 
Call:
lm(formula = y3 ~ x3, data = anscombe)
 
Residuals:
Min      1Q  Median      3Q     Max
-1.1586 -0.6146 -0.2303  0.1540  3.2411
 
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept)   3.0025     1.1245   2.670  0.02562 *
x3            0.4997     0.1179   4.239  0.00218 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
Residual standard error: 1.236 on 9 degrees of freedom
Multiple R-squared: 0.6663,	Adjusted R-squared: 0.6292
F-statistic: 17.97 on 1 and 9 DF,  p-value: 0.002176 

> reg3b=lm(y3~x3,data=anscombe[-3,])
> summary(reg3b)
 
Call:
lm(formula = y3 ~ x3, data = anscombe[-3, ])
 
Residuals:
Min         1Q     Median         3Q        Max
-0.0041558 -0.0022240  0.0000649  0.0018182  0.0050649
 
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.0056494  0.0029242    1370   <2e-16 ***
x3          0.3453896  0.0003206    1077   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
Residual standard error: 0.003082 on 8 degrees of freedom
Multiple R-squared:     1,	Adjusted R-squared:     1
F-statistic: 1.161e+06 on 1 and 8 DF,  p-value: < 2.2e-16 

> reg4=lm(y4~x4,data=anscombe)

This time, there is an other kind of outlier, in 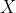's, but again, the regression is exactly the same,

> summary(reg4)
 
Call:
lm(formula = y4 ~ x4, data = anscombe)
 
Residuals:
Min     1Q Median     3Q    Max
-1.751 -0.831  0.000  0.809  1.839
 
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept)   3.0017     1.1239   2.671  0.02559 *
x4            0.4999     0.1178   4.243  0.00216 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
Residual standard error: 1.236 on 9 degrees of freedom
Multiple R-squared: 0.6667,	Adjusted R-squared: 0.6297
F-statistic:    18 on 1 and 9 DF,  p-value: 0.002165