Measuring Bias in Published Work
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
In a series of previous posts, I’ve spent some time looking at the idea that the review and publication process in political science—and specifically, the requirement that a result must be statistically significant in order to be scientifically notable or publishable—produces a very misleading scientific literature. In short, published studies of some relationship will tend to be substantially exaggerated in magnitude. If we take the view that the “null hypothesis” of no relationship should not be a point at but rather a set of substantively ignorable values at or near zero, as I argue in another paper and Justin Gross (an assistant professor at UNC-CH) also argues in a slightly different way, then this also means that the literature will tend to contain many false positive results—far more than the nominal
value of the significance test.
This opens an important question: is this just a problem in theory, or is it actually influencing the course of political science research in detectable ways?
To answer this question, I am working with Ahra Wu (one of our very talented graduate students studying International Relations and political methodology at Rice) to develop a way to measure the average level of bias in a published literature and then apply this method to recently published results in the prominent general interest journals in political science.
We presented our initial results on this front at the 2013 Methods Meetings in Charlottesville, and I’m sad to report that they are not good. Our poster summarizing the results is here. This is an ongoing project, so some of our findings may change or be refined as we continue our work; however, I do think this is a good time to summarize where we are now and seek suggestions.
First, how do you measure the bias? Well, the idea is to be able to get an estimate for and stat. sig.]. We believe that a conservative estimate of this quantity can be accomplished by simulating many draws of data sets with the structure of the target model but with varying values of
, where these
values are drawn out of a prior distribution that is created to reflect a reasonable belief about the pattern of true relationships being studied in the field. Then, all of the
estimates can be recovered from properly specified models, then used to form an empirical estimate of
and stat. sig.]. In essence, you simulate a world in which thousands of studies are conducted under a true and known distribution of
and look at the resulting relationship between these
and the statistically significant
.
The relationship that you get between |stat. sig] and
is shown in the picture below. To create this plot, we drew 10,000 samples (N = 100 each) from the normal distribution
for three values of
(we erroneously report this as 200,000 samples in the poster, but in re-checking the code I see that it was only 10,000 samples). We then calculated the proportion of these samples for which the absolute value of
is greater than 1.645 (the cutoff for a two-tailed significance test,
) for values of
.
As you can see, as gets larger, its bias also grows–which is a bit counterintuitive, as we expect larger
values to be less susceptible to significance bias: they are large enough such that both tails of the sampling distribution around
will still be statistically significant. That’s true, but it’s offset by the fact that under many prior distributions extremely large values of
are unlikely–less likely, in fact, than a small
that happened to produce a very large
! Thus, the bias actually rises in the estimate.
With a plot like this in hand, determining and stat. sig.] is a mere matter of reading the plot above. The only trick is that one must adjust the parameters of the simulation (e.g., the sample size) to match the target study before creating the matching bias plot.
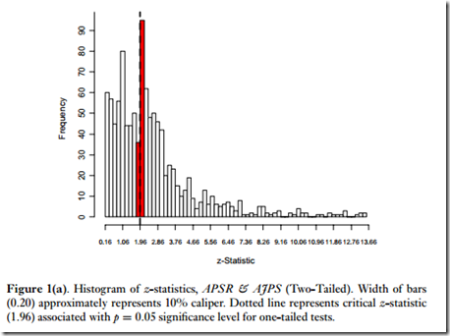
Concordantly, we examined 177 quantitative articles published in the APSR (80 articles in volumes 102-107, from 2008-2013) and the AJPS (97 articles in volumes 54-57, from 2010-2013). Only articles with continuous and unbounded dependent variables are included in our data set. Each observation of the collected data set represents one article and contains the article’s main finding (viz., an estimated marginal effect); details of how we identified an article’s “main finding” are in the poster, but in short it was the one we thought that the author intended to be the centerpiece of his/her results.
Using this data set, we used the technique described above to estimate the average % absolute bias, , excluding cases we visually identified as outliers. We used three different prior distributions (that is, assumptions about the distribution of true
values in the data set) to create our bias estimates: a normal density centered on zero (
), a diffuse uniform density between –1022 and 9288, and a spike-and-slab density with a 90% chance that
and a 10% chance of coming from the prior uniform density.
As shown in the Table below, our preliminary bias estimates for all of these prior densities hover in the 40-50% range, meaning that on average we estimate that the published estimates are 40-50% larger in magnitude than their true values.
| prior density | avg. % absolute bias |
| normal | 41.77% |
| uniform | 40% |
| spike-and-slab | 55.44% |
| *note: results are preliminary. |
I think it is likely that these estimates will change before our final analysis is published; in particular, we did not adjust the range of the independent variable or the variance of the error term to match the published studies (though we did adjust sample sizes); consequently, our final results will likely change. Probably what we will do by the end is examine standardized marginal effects—viz., t-ratios—instead of nominal coefficient/marginal effect values; this technique has the advantage of folding variation in
and
into a single parameter and requiring less per-study standardization (as t-ratios are already standardized). So I’m not yet ready to say that these are reliable estimates of how much the typical result in the literature is biased. As a preliminary cut, though, I would say that the results are concerning.
We have much more to do in this research, including examining different evidence of the existence and prevalence of publication bias in political science and investigating possible solutions or corrective measures. We will have quite a bit to say in the latter regard; at the moment, using Bayesian shrinkage priors seems very promising while requiring a result to be large (“substantively significant”) as well as statistically significant seems not-at-all promising. I hope to post about these results in the future.
As a parting word on the former front, I can share one other bit of evidence for publication bias that casts a different light on some already published results. Gerber and Malhotra have published a study arguing that an excess of p-values near the 0.05 and 0.10 cutoffs, two-tailed, is evidence that researchers are making opportunistic choices for model specification and measurement that enable them to clear the statistical significance bar for publication. But the same pattern appears in a scenario when totally honest researchers are studying a world with many null results and in which statistical significance is required for publication.
Specifically, we simulated 10,000 studies (each of sample size n=100) where the true DGP for each study j is ,
,
. The true value of
has a 90% chance of being set to zero and a 10% chance of being drawn from
(this is the spike-and-slab distribution above). Consquently, the vast majority of DGPs are null relationships. Correctly-specified regression models
are estimated on each simulated sample. The observed (that is, published—statistically significant) and true, non-null distribution of standardized
values (i.e., t-ratios) from this simulation are shown below.
This is a very close match for a diagram of t-ratios published in the Gerber-Malhotra paper, which shows the distribution of z-statistics (a.k.a. large-sample t-scores) from their examination of published articles in AJPS and APSR.
So perhaps the fault, dear reader, is not in ourselves but in our stars—the stars that we use in published tables to identify statistically significant results as being scientifically important.
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.