Sub-Gaussian property for the Beta distribution (part 2)
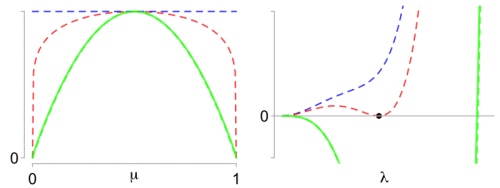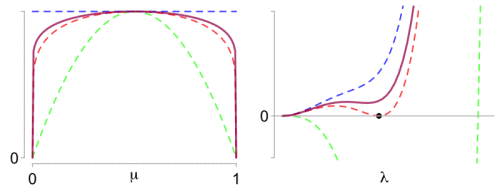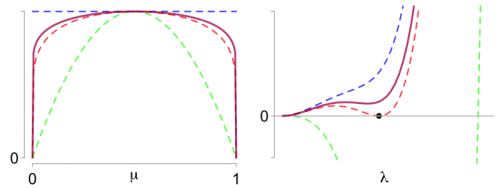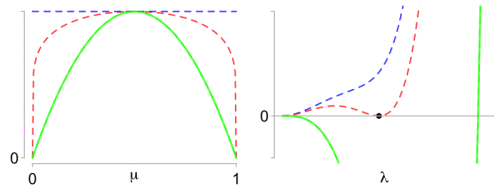
Left: What makes the Beta optimal proxy variance (red) so special? Right: The difference function has a double zero (black dot).
As a follow-up on my previous post on the sub-Gaussian property for the Beta distribution [1], I’ll give here a visual illustration of the proof.
A random variable with finite mean
is sub-Gaussian if there is a positive number
such that:
We focus on X being a Beta random variable. Its moment generating function
is known as the Kummer function, or confluent hypergeometric function
. So X is
-sub-Gaussian as soon as the difference function
remains positive on . This difference function
is plotted on the right panel above for parameters
. In the plot,
is varying from green for the variance
(which is a lower bound to the optimal proxy variance) to blue for the value
, a simple upper bound given by Elder (2016), [2]. The idea of the proof is simple: the optimal proxy-variance corresponds to the value of
for which
admits a double zero, as illustrated with the red curve (black dot). The left panel shows the curves with
varying, interpolating from green for
to blue for
, with only one curve qualifying as the optimal proxy variance in red.
References
[1] Marchal and Arbel (2017), On the sub-Gaussianity of the Beta and Dirichlet distributions. Electronic Communications in Probability, 22:1–14, 2017. Code on GitHub.
[2] Elder (2016), Bayesian Adaptive Data Analysis Guarantees from Subgaussianity, https://arxiv.org/abs/1611.00065
