Iterative OLS Regression Using Gauss-Seidel
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
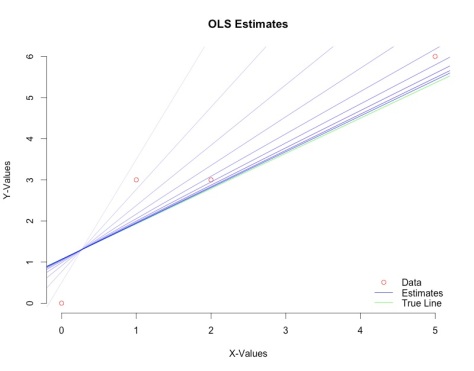
I just finished covering a few numerical techniques for solving systems of equations, which can be applied to find best-fit lines through a give set of data points.
The four points are arranged into an inconsistent system of four equations and two unknowns:
The system can be represented in matrix form:
The least-squares solution vector can be found by solving the normal equations
Solving for and
yields the following matrix system:
The system can be solved using Gauss-Seidel method.
Below, I run 10 iterations of Gauss-Seidel (visualized in the figure above). The estimated line gets successively closer to the true solution in green. The estimates are shown in blue – each iteration is shown in a darker shade than the next (see highlighted lines).
library(MASS) # package needed for ginv() function
A=cbind(c(4,8),c(8,30)) # coefficient matrix
b<-t(t(c(12,39))) # b-vector
x0<-t(t(c(0,0))) # starting vector
iter<-10 # number of Gauss-Seidel iterations to run
L<-lower.tri(A)*A # lower triang. A
U<-upper.tri(A)*A # upper triang. A
D<-diag(diag(A)) # diag of A
# plot points
xc<-c(0,1,2,5)
yc<-c(0,3,3,6)
plot(xc,yc,
col='red',
xlab="X-Values",
ylab="Y-Values",
bty='n')
title(main="OLS Estimates")
legend("bottomright",
c("Data","Estimates","True Line"),
lty=c(0,1,1),
pch=c(1,NA,NA),
col=c("red","blue","green"),
bty='n')
# create color palette - lines will get darker with each iter
pal<-colorRampPalette(c("#f2f2f2", "Blue"))
colors<-pal(iter) # creates color palette of length(iter)
# plot true line
abline(a=1.0714,b=.8571,col='green')
n<-1
while(n<=iter){
print(x0)
# Gauss-Seidel formula
x1<-(ginv((L+D)))%*%((-U%*%x0)+b)
x0<-x1
n=n+1
# plot estimated line
abline(a=as.numeric(x0[2,1]), # slope of estimated line
b=as.numeric(x0[1,1]), # y-intercept of estimated line
col=colors[n]) # pick nth color in palette
}
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
