Female hurricanes reloaded – another reanalysis of Jung et al.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
I have blogged a few days a ago about a study by Kiju Jung that suggested that implicit bias leads people to underestimate the danger of female-named hurricanes. The study used historical data to demonstrate a correlation between femininity and death-toll, and subsequent experiments seemed to show that people indeed estimate hurricanes to be less dangerous (all else equal) if they have more feminine names.
As you can read in my previous post, the study seemed rather convincing to me, if a bit surprising in its findings. But there was correlation in the regression, and there were the experiments which show why this correlation would occur. Plus, PNAS is a large journal, they would have this properly vetted, right? Anyway, I consider myself a rather cynical person when it comes to trust in statistical analyses, but my own “bullshit detectors were not twitching madly”, as did those of other people (see further critics here and here, and feel free to add links, I will sure have missed some).
Particularly the reanalysis of the regression on historical data by Bob O’Hara was sobering, as it suggested that the study failed to notice that hurricane damage affects death toll nonlinearly, and if one does include this in the models, femininity drops out as a predictor. I trust that Bob knows what he’s doing, so I would have given him the benefit of the doubt, but in the end I thought I’ll have a look at the data myself. The data is open, and Bob has his analysis commendably on GitHub, which I forked to my account.
Bob’s arguments were mainly based on looking at the residuals, and choosing that as a guideline for adding predictors. What I did is basically backing this up with a model selection to see how the different possible models compare, and if there are reasonable models that still have femininity of the name in there as a predictor. My full knitRed report is here, sorry, easier to leave everything on GitHub, but in a nutshell:
- I guess Bob is right, there should be a nonlinear term for damage added. There is consistently higher AICc for models that have such a term included. Btw., I get more support for a sqrt than for a quadratic term
- If we do this, femininity as a predictor is never in the best model, but models that include femininity stay within Delta AICc of 2. I would conclude from that that we have no smoking gun for an effect of femininity, but it’s also not completely excluded.
## Global model call: gam(formula = alldeaths ~ MasFem * (Minpressure_Updated.2014 + ## sqrt(NDAM) + NDAM + I(NDAM^2)), family = negbin(theta = c(0.2, ## 10)), data = Data[sqrt(Data$NDAM) < 200, ], na.action = "na.fail") ## --- ## Model selection table ## (Int) MsF Mnp_Upd.2014 NDA NDA^2 sqr(NDA) MsF:NDA ## 21 0.3439 -0.0001522 0.04794 ## 86 0.3341 -0.08935 -0.0001610 0.04874 2.861e-05 ## 25 0.5271 -3.468e-09 0.03524 ## 282 0.5197 -0.03425 -3.757e-09 0.03556 ## 150 0.3177 -0.16580 -0.0001650 0.04941 ## 22 0.3470 0.08015 -0.0001536 0.04795 ## 154 0.5172 -0.15170 -3.772e-09 0.03565 ## 23 3.3220 -0.003029 -0.0001482 0.04659 ## 29 0.3052 -0.0001907 9.577e-10 0.05092 ## 27 5.6880 -0.005271 -3.464e-09 0.03390 ## MsF:sqr(NDA) I(NDA^2):MsF df logLik AICc delta weight ## 21 3 -293.0 592.2 0.00 0.172 ## 86 5 -290.9 592.4 0.24 0.153 ## 25 3 -293.3 592.8 0.65 0.124 ## 282 1.358e-09 5 -291.1 592.9 0.69 0.122 ## 150 0.004055 5 -291.2 593.1 0.95 0.107 ## 22 4 -292.7 593.9 1.69 0.074 ## 154 0.003908 5 -291.7 594.1 1.86 0.068 ## 23 4 -292.9 594.2 1.99 0.064 ## 29 4 -292.9 594.4 2.16 0.058 ## 27 4 -293.0 594.4 2.21 0.057
Note that three outliers were removed for these results, which seemed sensible to me, but acts out in favor of femininity. Details in the report. The figure below shows the predictions of the best model that included femininity – the model predicts a practically relevant effect of femininity for high damage values. But as I noted in my report, we have very few data points for the high-damage region, so I think this is a VERY fragile result and I wouldn’t bet my money on it.
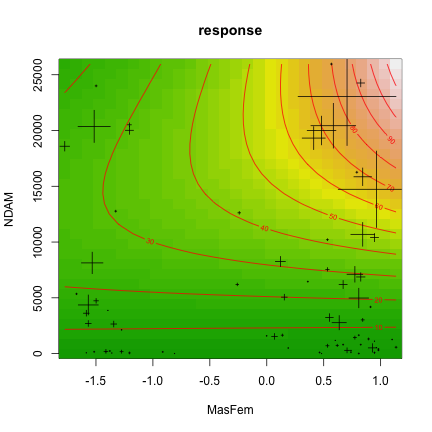
The fit of the best model that had femininity as a predictor included, Delta AIC 0.24, outliers removed. Crosses are the data values, size of the crosses is proportional to fatalities. Details see code
All in all, my conclusions from the statistical analysis based on the data in study is that I wouldn’t exclude the possibility that femininity could have an effect of a size that would make it relevant for policy, but there is no certainty about it at all.
I have read other comments that claimed that the data is wrong. I can’t say anything about that, but if that is so, it should be possible to establish that.
In general, assuming that the data was correct, I think the study isn’t quite as ridiculous as some portrayed it. I find it quite conceivable that there is an implicit bias that will affect our estimates of the severity of storms. The experiments seem to support that hypothesis, and they are easy enough to replicate, so people, please go out and do so. The more shaky question is how relevant this bias is for fatalities. Here, I would say the study is clearly overconfident in its analysis. I would conclude that the uncertainty range clearly includes zero, and I’m not quite sure what my best estimate would be … gut feeling: lower than the plot that I present above.
To end this on a general observation: what makes me a bit sad is knowing that, as for another recent study in PNAS where we wrote a reply, the authors would have probably found it much more challenging to place this study in PNAS if they would have done a more careful and conservative statistical analysis. I’m not saying that the competition for space in high-impact journals directly or indirectly encourages presenting results in an overconfident way – there are many examples in the history of Science of overconfidence and wishful thinking when the fight was not yet about journal space and tenure. But let’s say that there is a certain amount of noise in the analyses that are on the market place where studies are traded. High-impact journals are looking for the unexpected, and sometimes they may find it, but this also means that they will attract the outliers of this noise. As a consequence, at equal review quality, we can expect these journals to have more outliers (wrong results), and that I think is a problem because the publications in these journals decide careers and influence policy. I’m quite sure that the review in PNAS or Nature is as good as in any other journal, but given the previous arguments, it needs to be better than other journals, much better, specially on the side of the methods. A few practical ideas: maybe worth thinking about adjusting p-values or alpha values to journal impact, knowing that high-ranked journals implicitly get more studies offered than they publish, and thus implicitly test multiple hypothesis (implicitly all studies that are done, because if someone finds a high effect he/she sends it to a high journal). Also, the big journals should definitely find or hire statisticians to independently confirm the analysis of all papers the publish. And in general, it would be good to remember that extraordinary claims require extraordinary evidence.
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
