The study of food webs is very relevant, considering the role these networks have in describing the transfer of energy and matter in the ecosystem (Thompson et al. 2012). As such, the evaluation of the robustness to species extinctions is an important step in any analysis evaluating food web stability.

The attack on networks, such as food webs, can be random or targeted to hubs. Hubs are nodes – here species – with much higher number of (trophic) interactions. To do that I used the approach described in Bellingeri et al (2013). These authors define an Intentionality Index, varying from 0 to 1, according to which there is an increasing probability of removing hubs: I=0 (random extinctions), I=1 (preferentially extinguishing hubs).

The robustness of the food web is evaluated by the number of primary extinctions required to have 50% of the species in the food web as secondary extinctions (eq. 1). Robustness is computed by:

R50 = E/S (1)

Where E is the number of primary extinctions required to cause 50% of the species in the food web to get extinguished and S is the total number of nodes in the food web.

The probability of a node being extinguished, considering its degree (the number of interactions), is determined by a function from the family of exponential probability mass functions (eq. 2).

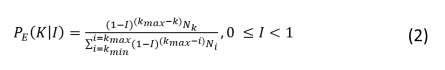
Where k is node degree, k_min and k_max are minimum and maximum number of trophic interactions in the food web nodes, N_k is the number of nodes with degree k and N_i is number of nodes with degree i (see Bellingeri et al. 2013 for details).

I will use my package FWebs, which is available on GitHub, to evaluate the robustness of food webs to species extinction (this is still a development version, suggestions, bug reports are welcome!).

First, installing and loading the package:

library(devtools) 
install_github("FMestre1/fw_package")
library(FWebs)

Then proceed to use one food web to evaluate its robustness to extinction.

#Create a food webs list, downloaded from the mangal database
mg1 <- create.fw.list(db="mg", ref=TRUE, spatial = TRUE)

#Convert to list a list of graph objects
graph_list1 <- convert.to.graph.list(mg1)

#Create a vector with the values for the Intentionality Index (I)
i_index <- seq(from = 0, to = 1, by =0.01)
i_index <- head(i_index,-1)

#Extract one food web to use as example
fw1 <- graph_list1[[40]]

#Compute the probability to remove each species (node) 
prob_exp <- exponent.removal(fw1, i_index)

#Simulate the extraction of species to evaluate how many primary extinctions are required to have 50% of the total species extinguished (using only 10 iterations for simplicity)
it1 <- iterate(fw_to_attack=fw1, prob_exp, alpha1=50, iter=10, i_index, plot = TRUE)

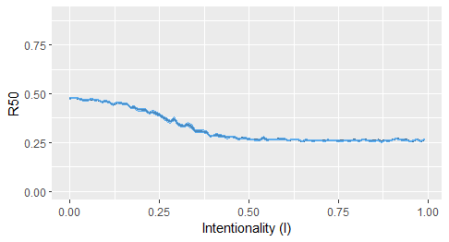
This post demonstrates a simple approach to evaluate the robustness of food webs to species extinction. It might be used in other types of ecological networks, or even non-ecological networks. Those interested can see the paper by Bellingeri, M. et al. (2013) for additional details.

References

Bellingeri, M. et al. (2013). Increasing the extinction risk of highly connected species causes a sharp robust-to-fragile transition in empirical food webs. Ecological Modelling, 251, 1-8.

Thompson, R.M. et al. (2012). Food webs: reconciling the structure and function of biodiversity. Trends in Ecology & Evolution, 27(12), 689-697.