Introduction

With the R6 library enabling users to create object classes, it is possible to solve a variety of computer science problems using R. Following the same fashion of my previous blogs on tree search algorithms (see here, here, here and here), in this blog I explore solving linked list problems using R.

The codes written here are based on Alvin the Programmer’s tutorial on linked list problems for technical interviews on the FreeCodecamp Youtube channel. So if you want to follow my learning experience, check out the video below. Thank you Alvin for making the educational content!

What is a linked list?

Using GeeksforGeeks’ definition, a linked list is a linear data structure, in which the elements are not stored at contiguous memory locations. The elements in a linked list are linked using pointers. In simple words, a linked list consists of nodes where each node contains a data field and a reference(link) to the next node in the list.

This can actually be visualized with the ggplot2 and ggdag packages.

library(tidyverse)
library(ggdag)

dagify(d~c,
       c~b,
       b~a) %>%
   tidy_dagitty() %>%
   mutate(x=c(1,2,3,4),
          y=c(1,1,1,1),
          xend=c(1.99,2.99,3.99,NA),
          yend=c(1,1,1,NA)) %>% 
  ggdag()+
  theme_dag()+
  ylim(0.95,1.10)+
  annotate("text", x=1, y=1.02,label="Head")+
  annotate("text", x=4, y=1.02,label="Tail")+
  annotate("text", x=1.5, y=0.995,label="next")+
  annotate("text", x=2.5, y=0.995,label="next")+
  annotate("text", x=3.5, y=0.995,label="next")+
  annotate("text", x=1, y=0.98,label="node")+
  annotate("text", x=2, y=0.98,label="node")+
  annotate("text", x=3, y=0.98,label="node")+
  annotate("text", x=4, y=0.98,label="node")+
  ggtitle("A Linked List")+
  theme(plot.title=element_text(hjust=0.5, vjust=-45))

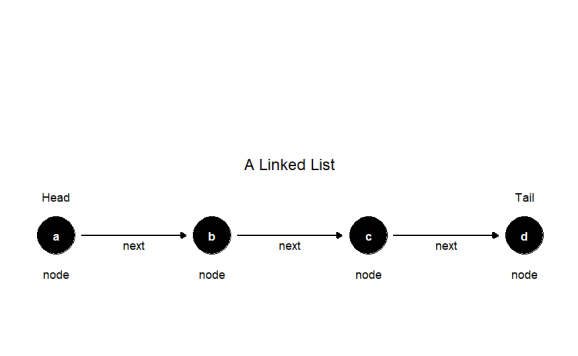
While the above data structure appears to be simple enough. There are a variety of problems which can be presented with it. Using the R6 library the above linked list can be constructed with the following code.

library(R6)

# Node constructor
node <- R6Class("Node", 
                list(
                  val=NULL,
                  nxt = NULL, 
                  initialize = function(val=NULL,
                                        nxt=NULL){
                    self$val <- val
                    self$nxt <-nxt
                  }
                )
                )

# Make our nodes
a <- node$new(val="a")
b <- node$new(val="b")
c <- node$new(val="c")
d <- node$new(val="d")

# Link them together
a$nxt<- b
b$nxt<- c
c$nxt<- d

# a -> b -> c -> d -> NULL

With the linked list created, lets explore answering problems involving linked lists. For completeness, iterative and recursive solutions are be provided.

1. Linked List Traversal

Traversing a linked list involves writing code that will visit each node of the list once and terminate at the end of the list. The iterative solution involves setting a current node and employing a while loop. The recursive solution just requires a if statement to check if the node is null.

# Iterative code
traversal <- function(node){
 current <- node

 while(!is.null(current[['val']])){
   print(current[['val']])
   current<- current[['nxt']]
 }
}

traversal(a)


## [1] "a"
## [1] "b"
## [1] "c"
## [1] "d"


traversal_recursive<- function(node){

  if(is.null(node[["val"]])){
    return()
  }
  print(node[['val']])
  traversal_recursive(node[["nxt"]])
}

traversal_recursive(a)


## [1] "a"
## [1] "b"
## [1] "c"
## [1] "d"

## NULL

My one annoyance with the recursive solution is that NULL is explicitly returned in the console output, but besides for that, I find it a much cleaner solution than its iterative counterpart.

2. Linked List Values

Getting a linked list’s values is a direct application of the traversal. Recall, that the linked list is an object whose values are not readily accessible, as such a solution for getting those values is required.

# Linked List values


listValues <- function(node){
  current <- node
  values <- c()
  while(!is.null(current[['val']])){
    values<- c(values,current[['val']])
    current<- current[['nxt']]
  }
  return(values)
}

listValues(a)


## [1] "a" "b" "c" "d"


listValues_recursive <- function(node){
  if(is.null(node[["val"]])){
    return()
  }
  values<-node[['val']]
  values<-append(values,listValues_recursive(node[["nxt"]]))

  return(values)

}

listValues_recursive(a)


## [1] "a" "b" "c" "d"

Both solutions give the same output. If you understand recursion then the recursive code gives a cleaner solution.

3. Sum of Linked List Values

In this problem, numeric values are assigned to the list’s nodes. The challenge is to get the sum of all the node values. Since we know how to do a list traversal, getting the sum of the list’s nodes is also a direct application of it. The code below first creates a linked list with values assigned to each node and the iterative and recursive solutions are offered.

# Make our nodes with numbers
a <- node$new(val=8)
b <- node$new(val=7)
c <- node$new(val=2)
d <- node$new(val=1)

# Link them together
a$nxt<- b
b$nxt<- c
c$nxt<- d



# Iterative Solution


sumList <- function(node){
  current <- node
  total <- 0 
  while(!is.null(current[['val']])){
    total<- total + current[['val']]
    current<- current[['nxt']]
  }
  return(total)
}

sumList(a)


## [1] 18


# Recursive solution


sumList_recursive<- function(node){
  if(is.null(node[["val"]])){
    return(0)
  }

  return(node[['val']] + sumList_recursive(node[['nxt']]))
}


sumList_recursive(a)


## [1] 18

4. Check if Value is in Linked List

Applying the same concept of traversal, this algorithm checks if a given value is assigned to a node in a linked list by iteratively (or recursively) looking at each value in the linked list. If there is a match, the algorithm terminates and returns TRUE, otherwise the algorithm searches to the end of the list and returns FALSE. The iterative and recursive solutions are shown below:

# Remake linked List
a <- node$new(val="a")
b <- node$new(val="b")
c <- node$new(val="c")
d <- node$new(val="d")

# Link them together
a$nxt<- b
b$nxt<- c
c$nxt<- d

# Iterative Solution

inList <- function(node,target){
  current<-node
  while(!is.null(current[['val']])){
   if(current[["val"]] == target){
     return(TRUE)
   }else{
     current <-current[['nxt']]
   }
  }
  return(FALSE)
}

# Test cases
inList(a,'c')


## [1] TRUE


inList(a,'g')


## [1] FALSE


# Recursive solution


inList_recursive <- function(node,target){
  if(is.null(node[["val"]])){
    return(FALSE)
  }
  if(node[['val']]==target){
    return(TRUE)
  }
  inList_recursive(node[['nxt']],target)
}


# Test cases
inList_recursive(a,'c')


## [1] TRUE


inList_recursive(a,'g')


## [1] FALSE

5. Get Node Value

This problem involves creating a function which will allow us to access each node in a linked list based on its index. If we were using a more traditional programming language we would start our index from 0. However with R we start from 1. The iterative and recursive solutions are listed below.

# Iterative Solution


nodeValue<-function(node, index){
    # Count value
    i <- 1
    current<-node

    while(!is.null(current[["val"]])){
      if(i==index){
        return(current[["val"]])
      }
      # Increment
      current<-current[["nxt"]]
      i <- i+1
      }
      return(NULL)

  }


# Test Cases
nodeValue(a,2)


## [1] "b"


nodeValue(a,1)


## [1] "a"


nodeValue(a,3)


## [1] "c"


nodeValue(a,4)


## [1] "d"


nodeValue(a,6)


## NULL


# Recursive Solution


nodeValue_recursive<- function(node,index){
  if(is.null(node[["val"]])){
    return(NULL)
  }
  if(index==1){
    return(node[["val"]])
  }
  nodeValue_recursive(node[['nxt']],index-1)
}

# Test Cases
nodeValue_recursive(a,2)


## [1] "b"


nodeValue_recursive(a,1)


## [1] "a"


nodeValue_recursive(a,3)


## [1] "c"


nodeValue_recursive(a,4)


## [1] "d"


nodeValue_recursive(d,6)


## NULL

6. Linked List Reversal

One of the more popular problems presented in a coding interview (so I was told) is the problem of “reversing” a linked list. This involves writing code which will reverse the order of the list’s nodes. To solve this, we need to declare a variable which will store a nodes “next” value as its previous value and work iteratively (or recursively) across the list. Since the algorithm starts from the beginning of the list, the first previous value is defined as NULL.

The iterative solution is:

reverseList<- function(node){
  prev<- NULL
  current<- node
  while(!is.null(current)){
    nxt<-current[['nxt']]
    current[['nxt']]<-prev
    prev <-current
    current<-nxt
  }
  return(prev)
}

# Reverse the list and check if the list was reversed
reverseList(a) %>% listValues()


## [1] "d" "c" "b" "a"

Its important to note that the list reversal affects each of the node properties and the list as a whole. If we look at node a we see that its next value is NULL.

# a's nxt value is null
a


## <Node>
##   Public:
##     clone: function (deep = FALSE) 
##     initialize: function (val = NULL, nxt = NULL) 
##     nxt: NULL
##     val: a

As such, for the recursive reversal we will restore the linked list to its original form by reversing from the d node.

reverseList_recursive<- function(node,prev=NULL){
  if(is.null(node)){
    return(prev)
  }
  nxt<-node[['nxt']]
  node[['nxt']]<-prev
  reverseList_recursive(nxt,node)
}

# Reverse the list from the `d` node and check if the list was reversed

reverseList_recursive(d) %>% listValues()


## [1] "a" "b" "c" "d"

7. Zipper Lists

The zipper lists problem involves two lists where the goal is to “zip” the two lists together by creating a single list with alternating nodes from each list. If the lists differ in size, then when there are no other nodes left in the shorter list, the rest of the nodes in the longer list is appended to the end of the zipped list. This is shown visually with with the visual below:

library(ggpubr)

ggarrange(
  dagify(d~c,
       c~b,
       b~a,
       q~r) %>%
   tidy_dagitty() %>%
   mutate(x=c(1,2,3,1,4,2),
          y=c(1.5,1.5,1.5,1.1,1.5,1.1),
          xend=c(1.99,2.99,3.99,1.99,NA,NA),
          yend=c(1.5,1.5,1.5,1.1,NA,NA)) %>% 
  ggdag()+
  theme_dag()+
  ylim(0.95,2)+
  ggtitle("Linked Lists- Pre-Zipping")+
  theme(plot.title=element_text(hjust=0.5, vjust=-10)),

dagify(d~c,
       c~r,
       r~b,
       b~q,
       q~a) %>%
   tidy_dagitty() %>% 
   mutate(x=c(1,3,5,2,4,6),
          y=c(1,1,1,1,1,1),
          xend=c(1.99,3.99,5.99,2.99,4.99,NA),
          yend=c(1,1,1,1,1,NA)) %>% 
  ggdag()+
  theme_dag()+
  ggtitle("Zipped List")+
  theme(plot.title=element_text(hjust=0.5, vjust=-10)),
 nrow = 2
)

The iterative code for this solution is:

# First lets make our two separate lists
##########
# List 1 #
##########
a <- node$new(val="a")
b <- node$new(val="b")
c <- node$new(val="c")
d <- node$new(val="d")
# Link them together
a$nxt<- b
b$nxt<- c
c$nxt<- d

##########
# List 2 #
##########

q <-node$new(val="q")
r<- node$new(val="r")

q$nxt<-r

zipList<- function(node1,node2){
  end <- node1
  current1 <- node1[['nxt']]
  current2 <- node2
  # Count
  i <- 0

  while(!is.null(current1) & !is.null(current2)){
    if(i%%2==0){
      end[["nxt"]]<-current2
      current2<- current2[["nxt"]]
    }else{
      end[["nxt"]]<-current1
      current1<- current1[["nxt"]]
    }

    end<- end[["nxt"]]
    #increment count
    i<- i+1
  }

  if(!is.null(current1)){
    end[["nxt"]]<-current1
  }

  if(!is.null(current2)){
    end[["nxt"]]<-current2
  }
  return(node1)
}

# list the values to ensure the operation has been preformed properly
zipList(a,q) %>% listValues()


## [1] "a" "q" "b" "r" "c" "d"

Since the linked lists have now been altered with the above operation. To show the iterative solution the linked lists will have to be reconstructed. The recursive solution is:

zipList_recursive<- function(node1,node2){
  if(is.null(node1) & is.null(node2)){
    return()
  }
  if(is.null(node1)){
    return(node2)
  }
  if(is.null(node2)){
    return(node1)
  }
  next1 <- node1[['nxt']]
  next2 <- node2[['nxt']]

  node1[['nxt']]<-node2
  node2[['nxt']]<-zipList_recursive(next1,next2)

  return(node1)
}


# Remake Linked Lists

##########
# List 1 #
##########
a <- node$new(val="a")
b <- node$new(val="b")
c <- node$new(val="c")
d <- node$new(val="d")
# Link them together
a$nxt<- b
b$nxt<- c
c$nxt<- d

##########
# List 2 #
##########

q <-node$new(val="q")
r<- node$new(val="r")

q$nxt<-r

# list the values to ensure the operation has been preformed properly
zipList_recursive(a,q) %>% listValues()


## [1] "a" "q" "b" "r" "c" "d"

Conclusion

I’ve said it before, the R6 library changes the R language from being simply a statistical computing language to a proper programming language. The more I learn about R the more I see that there is so much more possible with it.

Thank you for reading my blog! I actually was working on this piece before my previous blog on creating a blockchain but I got distracted. If you enjoyed this content be sure to subscribe to my mailing list and all donations are happily accepted as well. Thanks again!