When you are in 101 of risk management is usual to confuse Bar, VAR and VaR, the first one refers to a place that you should buy (it is a bad idea, do not do it), the second is Vector Autoregressive and the last one Value at Risk, our matter.

What is Value at Risk?

In simple words, it is the maximum possible loss of your money in a period and the formal definition is:

VaR is a method of assessing risk that uses standard statistical techniques used routinely in other technical fields. Loosely, VAR summarizes the worst loss over a target horizon that will not be exceeded with a given level of confidence.

(Jorion, 2007)

How to compute?

There are two methods to compute

• Parametric
• No Parametric

The parametric method assumes that the returns follow a normal distribution, hence the VaR of a portfolio is:

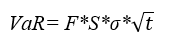
F         Factor of confidence level

S          Total amount of the investment

σ          Volatility

R Code

library(pacman) p_load(tidyverse,tidyquant)

Import dataset Technical Trading Rule Composite Data

data(ttrc) data <- as_tibble(ttrc)

Select Close prices

close <- data %>% select(Close)

Parametric VaR function

VaRP <- function(x,p,s,t){ x1 <- as.numeric(unlist(x)) r1 <- (x1/lag(x1))-1 r1 <- as.numeric(unlist(r1)) sig<- sd(r1,na.rm = T) p <- as.numeric(qnorm(p)) h <- sqrt(t/252) pvar <- sig*p*h*s print(paste("The VaR is $",prettyNum(pvar,big.mark = ","))) }

Arguments

x          Object that contains close prices

p          Percent confidence level

s          Total amount of the investment

t           Time horizon (days)

Example

Using the close prices of ttrc , we want to know the VaR of $ 100 million, with a holding period of 7 days and 99 confidence level

VaRP(close,.99,100000000,7)

[1] "The VaR is $ 552,757"

There is a simple way to compute parametric VaR. I know you can improve it. In future posts I am going to show how to compute with no parametric methods.

Reference

De Lara, A. (2018) Medición y control de riesgos financieros. México: Limusa

Jorion, P. (2007). Value at Risk. McGraw Hill.