Hold the Phones . . . Stanton’s Alive Again
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
Sometimes, events move faster than we predict them. This is one of the things that makes statistics as much of an art as a science. Last night, Giancarlo Stanton hit not 1 but 2 home runs. He is now tied with Babe Ruth’s old record of 59 home runs in a single season. So, my fairly negative prediction of last night needs a drastic revision. He only needs 2 more dingers to equal Maris’ mark and he still has 6 games to do it.
As I write this, I’m waiting for Sports Illustrated’s site to update its hitting database (the source of numbers for Jim Albert’s model). However, I’ve been thinking more about Bob Carpenter’s concise model and its Poisson estimation for the number of at bats that Stanton is likely to have. Here is the Carpenter model updated with last night’s numbers.
ab <- 583
hr <- 59
games <- 156
phrs <- sum(rbinom(1e5,
rpois(1e5, 10 * ab / games),
rbeta(1e5, 1 + hr, 1 + ab - hr)) >= (61 - hr)) / 1e5
print(paste("Probability of tying or breaking the record:",
round(phrs, 3)))
[1] "Probability of tying or breaking the record: 0.888"
In this model, the probability of success (tying or breaking the record) has exploded to 0.888. This has a lot to do with the number of at bats, the random poisson simulation encapsulated in the Poisson distribution estimation of the number of trials (the second parameter of the binomial estimator, ‘rbinom’). Let’s look at this value across the 100,000 simulations that Carpenter makes:
new_abs <- rpois(1e5, 10 * ab / games)
print(paste("Estimated number of remaining at bats:",
round(mean(new_abs), 2)))
## [1] "Estimated number of remaining at bats: 37.38"
summary(new_abs)
Min. 1st Qu. Median Mean 3rd Qu. Max.
13.00 33.00 37.00 37.38 41.00 67.00
# Show histogram of at bat distribution
suppressPackageStartupMessages(library(ggpubr))
nab <- tibble(new_abs)
gghistogram(nab, x = "new_abs", binwidth = 1, add = "mean",
add_density = TRUE, ggtheme = theme_gray(), fill = "gray",
title = "Distribution of New At Bats for Stanton",
xlab = "New At Bats")
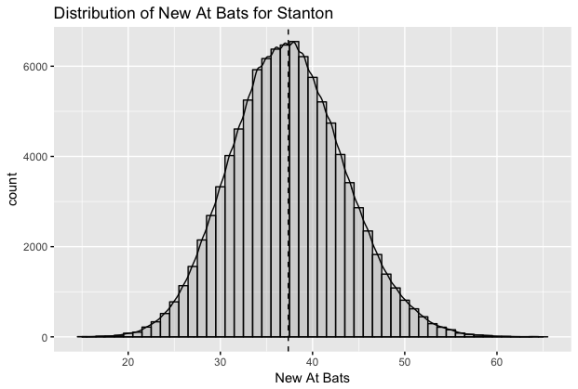
This simulation suggests that Stanton will have more or less 37 at bats remaining in six games. That’s an average of 6 at bats per game. I’ve never heard of a series of six games that are either so long (in terms of extra innings) or with so many runs for a mediocre team like the Marlins that batters would get an average of 6 at bats per game.
Also, it is important to remember that we are measuring at bats here, not plate appearances. Plate appearances are the actual number of times the batter comes to the plate to bat. At bats reduce that number as they do not count base on balls, hit by pitch and other categories.
Let us try a revised version of the Carpenter model that limits the at bats to a more realistic 4 per game, or 24 for the remainder of the season. Here we see that the probability of tying or breaking the record is a bit reduced to 0.714.
at_bats_game <- 4
phrs2 <- sum(rbinom(1e5,
at_bats_game * (162 - games),
rbeta(1e5, 1 + hr, 1 + ab - hr))
>= (61 - hr)) / 1e5
print (paste("Revised prob. of tying or breaking the record:", round (phrs2, 3)))
## [1] "Revised prob. of tying or breaking the record: 0.714"
This probability is still quite high and not very believable given some basic feel for the game. As well, the probability of hitting a home run on any given at bat (the ‘rbeta’ estimate of the probability of success in any binomial trial) is overestimated. Assigning parameters α (alpha) and β (beta) to the beta distribution requires some more experimentation. Both (1 + hr) and (1 + ab – hr) are both reasonable starting points. Many Bayesian tutorials would recognize these as good estimates for a true Bayesian model that calculates a posterior probability based on a prior probability and evidence (how many home runs Stanton has hit so far in x at bats and y games), this is not a true Bayesian model. The ‘rbeta’ function is calculating an initial probability not a posterior. It is merely the p term in the ‘rbinom’ function.
‘rbinom’ requires three parameters as shown below:
rbinom(simulations, trials, probability)
Simulations is the number of times we are going to repeat the experiment. In this case, it means how many times are we going to simulate Stanton’s 24 remaining at bats. Trials is the number of at bats in each experiment. Probability is the probability of success in any one trial. There is no second, posterior probability in this model. While there is no overriding necessity to use the rbeta function, it turns out it performs fairly well. Let’s compare it to using a frequentist approach and substituting Stanton’s real home run rate (close to 1 home run per 10 at bats) for the rbeta function.
phrs3 <- sum(rbinom(1e5,
at_bats_game * (162 - games),
hr / ab)
>= (61 - hr)) / 1e5
print(paste("Revised prob. of tying or breaking the record:", round(phrs3, 3)))
[1] "Revised prob. of tying or breaking the record: 0.715"
As we can see, the rbeta gives us virtually the same answer as Stanton’s existing home run hitting rate.
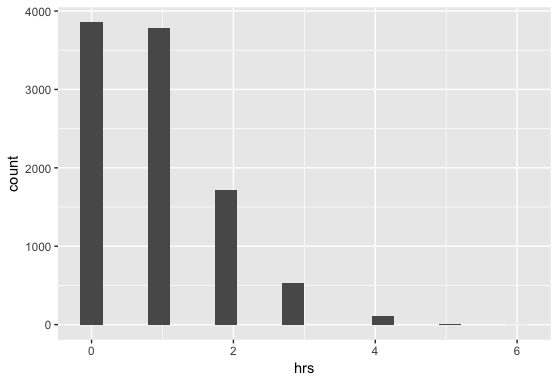
Let’s now look at the Albert model and see if it has become more optimistic about Stanton’s chances. Albert’s estimate has increased to 23.6% from 3%. So, the two new homers have had a significant effect on its view of Stanton’s chances. However, over its 10,000 simulations, it believes that Stanton will only hit one additional homer, leaving him in limbo without a share of the record. Given the model’s standard deviation of almost 1 home run, it suggests that Stanton could tie with Maris at 61. However, it is still more pessimistic than Carpenter’s model. As you can see from the graph below, the simulations in Albert’s model suggest that 0 and 1 home runs are the most likely outcomes in the 10,000 simulations. The 2 or greater options account for the 23.6% cited above.
R is an amazing tool for conducting these analyses. To do the number of variations I’ve experimented with while writing this post, I’ve modified Jim Albert’s code somewhat. Since he wrote it clearly, it was a piece of cake to mold it to my purposes (largely to avoid wasting time scraping the web on each variation I tried since once the data is downloaded, it’s only going to be updated after the next game).
So, 23.6% or 71.5% probability of tying or breaking Maris’ record. Which is correct? I lean toward Albert’s analysis. As the race between Maris and Mickey Mantle in 1961 showed, there are many factors, physical and psychological, that affect players’ performance at the end of a six-month season.
Let’s see what happens Sunday. Until then, if you want to see the R code I’ve used for this, have a look at this file: Stanton_HR_Prediction_v2a .
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
