Like many data nerds, I’m a big fan of Tyler Vigen’s Spurious Correlations, a humourous illustration of the old adage “correlation does not equal causation”. Technically, I suppose it should be called “spurious interpretations” since the correlations themselves are quite real, but then good marketing is everything.

There is, however, a more formal definition of the term spurious correlation or more specifically, as the excellent Wikipedia page is now titled, spurious correlation of ratios. It describes the following situation:

1. You take a bunch of measurements X1, X2, X3…
2. And a second bunch of measurements Y1, Y2, Y3…
3. There’s no correlation between them
4. Now divide both of them by a third set of measurements Z1, Z2, Z3…
5. Guess what? Now there is correlation between the ratios X/Z and Y/Z

It’s easy to demonstrate for yourself, using R to create something like the chart in the Wikipedia article.

First, create 500 observations for each of x, y and z.

library(ggplot2)

set.seed(123)
spurious_data <- data.frame(x = rnorm(500, 10, 1),
                            y = rnorm(500, 10, 1),
                            z = rnorm(500, 30, 3))

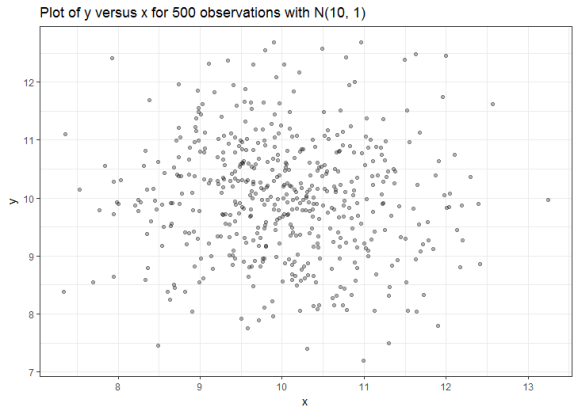
Next, convince yourself that x and y are uncorrelated.

cor(spurious_data$x, spurious_data$y)
# [1] -0.05943856
spurious_data %>% ggplot(aes(x, y)) + geom_point(alpha = 0.3) + 
theme_bw() + labs(title = "Plot of y versus x for 500 observations with N(10, 1)")

Finally, repeat step 2 after dividing x and y through by z.

cor(spurious_data$x / spurious_data$z, spurious_data$y / spurious_data$z)
# [1] 0.4517972
spurious_data %>% ggplot(aes(x/z, y/z)) + geom_point(aes(color = z), alpha = 0.5) +
 theme_bw() + geom_smooth(method = "lm") + 
scale_color_gradientn(colours = c("red", "white", "blue")) + 
labs(title = "Plot of y/z versus x/z for 500 observations with x,y N(10, 1); z N(30, 3)")

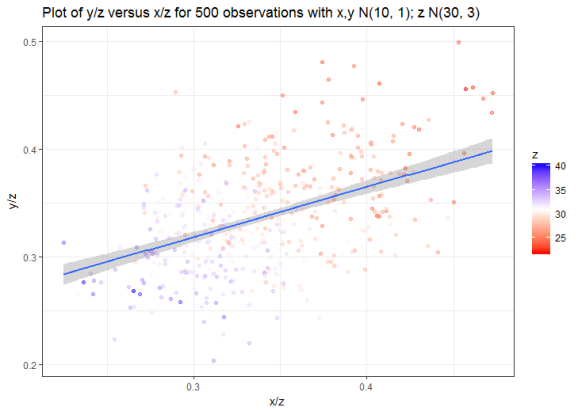
This effect is reasonably intuitive: dividing both x and y by the same z forces them into the range (0,1). Larger values for z push x/z and y/z towards lower values, smaller values of z push them towards higher values. Visually though, it’s quite a striking effect which is even more pronounced if we increase the standard deviation for z.

spurious_data$z <- rnorm(500, 30, 6)
cor(spurious_data$x / spurious_data$z, spurious_data$y / spurious_data$z)
# [1] 0.8424597
spurious_data %>% ggplot(aes(x/z, y/z)) + geom_point(aes(color = z), alpha = 0.5) + 
theme_bw() + geom_smooth(method = "lm") + 
scale_color_gradientn(colours = c("red", "white", "blue")) + 
labs(title = "Plot of y/z versus x/z for 500 observations with x,y N(10, 1); z N(30, 6)")

Which looks an awful lot like a chart that I found recently in a published article that I was reading at work. Note that both axes are rates between 0-100 (percentages), suggesting that values were divided by a common divisor.

Should you wish to compare ratios or “relative” measurements, consult this reference and take a look at the R package propr, which implements methods for proportionality.