Veterinary Epidemiologic Research: Linear Regression Part 2 – Checking assumptions
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
We continue on the linear regression chapter the book Veterinary Epidemiologic Research.
Using same data as last post and running example 14.12:
tmp <- tempfile()
download.file("http://ic.upei.ca/ver/sites/ic.upei.ca.ver/files/ver2_data_R.zip", tmp) # fetch the file into the temporary file
load(unz(tmp, "ver2_data_R/daisy2.rdata")) # extract the target file from the temporary file
unlink(tmp) # remove the temporary file
### some data management
daisy2 <- daisy2[daisy2$h7 == 1, ] # we only use a subset of the data
library(Hmisc)
daisy2 <- upData(daisy2, labels = c(region = 'Region', herd = 'Herd number',
cow = 'Cow number',
study_lact = 'Study lactation number',
herd_size = 'Herd size',
mwp = "Minimum wait period for herd",
parity = 'Lactation number',
milk120 = 'Milk volume in first 120 days of lactation',
calv_dt = 'Calving date',
cf = 'Calving to first service interval',
fs = 'Conception at first service',
cc = 'Calving to conception interval',
wpc = 'Interval from wait period to conception',
spc = 'Services to conception', twin = 'Twins born',
dyst = 'Dystocia at calving',
rp = 'Retained placenta at calving',
vag_disch = 'Vaginal discharge observed',
h7 = 'Indicator for 7 herd subset'),
levels = list(fs = list('No' = 0, 'Yes' = 1),
twin = list('No' = 0, 'Yes' = 1),
dyst = list('No' = 0, 'Yes' = 1),
rp = list('No' = 0, 'Yes' = 1),
vag_disch = list('No' = 0, 'Yes' = 1)),
units = c(milk120 = "litres"))
library(lubridate)
daisy2$date <- as.character(daisy2$calv_dt)
daisy2$date <- ymd(daisy2$date)
daisy2$mth <- month(daisy2$date)
# calving in automn or not:
daisy2$aut_calv <- with(daisy2, ifelse(mth %in% c(9:12), "fall", "other"))
# centering variables:
daisy2$hs100 <- daisy2$herd_size / 100
daisy2$hs100_ct <- daisy2$hs100 - mean(daisy2$hs100)
daisy2$hs100_ctsq <- daisy2$hs100_ct^2
daisy2$parity_sc <- daisy2$parity - mean(daisy2$parity)
daisy3 <- daisy2[complete.cases(daisy2), ] # df with only complete cases
lm.wpc <- lm(wpc ~ aut_calv + hs100_ct + hs100_ctsq + parity_sc + twin +
+ dyst + rp + vag_disch + rp*vag_disch, data = daisy3)
(lm.wpc.sum <- summary(lm.wpc))
Call:
lm(formula = wpc ~ aut_calv + hs100_ct + hs100_ctsq + parity_sc +
twin + dyst + rp + vag_disch + rp * vag_disch, data = daisy3)
Residuals:
Interval from wait period to conception
Min 1Q Median 3Q Max
-76.40 -35.23 -15.22 22.64 210.63
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 66.9831 2.4970 26.825 < 2e-16 ***
aut_calvother -6.1336 2.6420 -2.322 0.020385 *
hs100_ct 21.8485 2.2546 9.690 < 2e-16 ***
hs100_ctsq 11.7763 3.1952 3.686 0.000236 ***
parity_sc 1.1421 0.8727 1.309 0.190848
twinYes 19.7621 9.8677 2.003 0.045387 *
dystYes 11.0347 5.5386 1.992 0.046515 *
rpYes 7.1111 4.8654 1.462 0.144067
vag_dischYes 2.0977 7.2588 0.289 0.772629
rpYes:vag_dischYes 19.9543 12.7239 1.568 0.117031
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 50 on 1515 degrees of freedom
Multiple R-squared: 0.07355, Adjusted R-squared: 0.06805
F-statistic: 13.36 on 9 and 1515 DF, p-value: < 2.2e-16
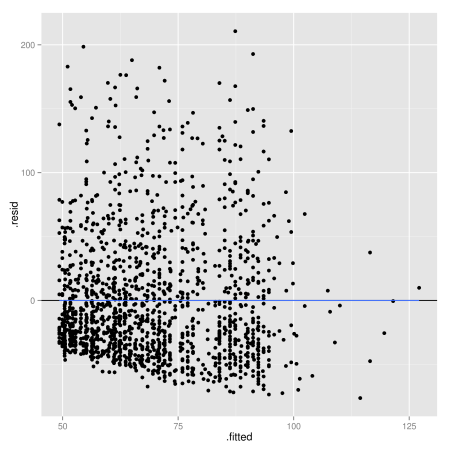
Now we can create some plots to assess the major assumptions of linear regression. First, let’s have a look at homoscedasticity, or constant variance of residuals. You can run a statistical test, the Cook-Weisberg test (or Breusch-Pagan test), available in libraries car and lmtest:
library(car) ncvTest(lm.wpc) Non-constant Variance Score Test Variance formula: ~ fitted.values Chisquare = 23.08052 Df = 1 p = 1.553565e-06 library(lmtest) bptest(lm.wpc) studentized Breusch-Pagan test data: lm.wpc BP = 24.3082, df = 9, p-value = 0.00384
Both tests are significant indicating the presence of heteroscedasticity but they are slightly different. Quoting John Fox from this post: “bp.test() performs the same score test as ncvTest(), except that the default alternative hypothesis is different — in bp.test() the error variance is a function of a linear combination of the regressors and in ncvTest() the error variance is a function of the fitted values (i.e., a *particular* linear combination of regressors). Testing against the fitted values with 1 df will have greater power if this is the real pattern of heteroscedasticity”.
But the evaluation of linear model assumptions relies more often on graphical methods. You can use the 6 diagnostic plots readily available after fitting your model, or try it with ggplot2 using the fortify() method which allow combining a model with its data (“the model fortifies the data, and the data fortifies the model”):
plot.lm(lm.wpc, which = 1) # diag plot in base stats package library(ggplot2) ggplot(lm.wpc, aes(.fitted, .resid)) + geom_hline(yintercept = 0) + geom_point() + geom_smooth(se = FALSE)
We can check the normality of the residuals by a statistical test, the Shapiro-Wilk test, and a normal probability plot (Q-Q plot):
shapiro.test(resid(lm.wpc)) Shapiro-Wilk normality test data: resid(lm.wpc) W = 0.8817, p-value < 2.2e-16 ggplot(lm.wpc, aes(sample = .stdresid)) + stat_qq() + geom_abline()
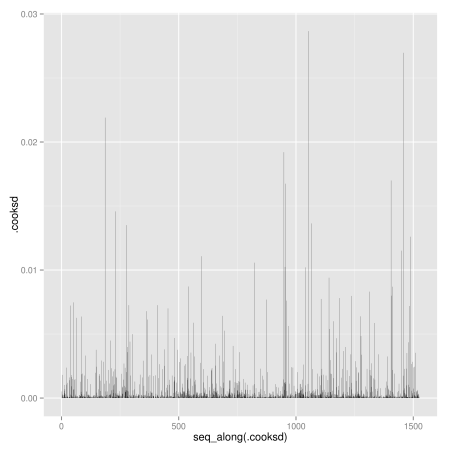
Other diagnostic plots: Scale-Location plot of sqrt(|residuals|) against fitted values, Cook’s distance plot, Residuals vs. leverages, Cook’s distances vs. leverages:
## Scale-Location plot of sqrt(|residuals|) against fitted values (which = 3)
ggplot(lm.wpc, aes(.fitted, abs(.stdresid))) +
geom_point() +
geom_smooth(se = FALSE) +
scale_y_sqrt()
# Cook's distance plot (which = 4)
ggplot(lm.wpc, aes(seq_along(.cooksd), .cooksd)) +
geom_bar(stat = "identity")
# Residuals vs. leverages (which = 5)
ggplot(lm.wpc, aes(.hat, .stdresid)) +
geom_vline(size = 2, colour = "white", xintercept = 0) +
geom_hline(size = 2, colour = "white", yintercept = 0) +
geom_point() +
geom_smooth(se = FALSE)
# Cook's distances vs leverages/(1-leverages) (which = 6)
ggplot(lm.wpc, aes(.hat, .cooksd)) +
geom_vline(colour = NA) +
geom_abline(slope = seq(0, 3, by = 0.5), colour = "white") +
geom_smooth(se = FALSE) +
geom_point()
You could also check the linearity of the predictor-outcome association by plotting the residuals against each of the continuous predictor variables, for example here centered herd size:
ggplot(lm.wpc, aes(hs100_ct, .resid)) + geom_point() + geom_smooth(method = "loess", se = FALSE)
Log Transformation
Let’s do a log transformation (with a simpler model) and back-transform the coefficients:
daisy3$milk120.sq <- daisy3$milk120^2
lm.wpc2 <- lm(wpc ~ vag_disch + milk120 + milk120.sq, data = daisy3)
lm.lwpc <- lm(log(wpc) ~ vag_disch + milk120 + milk120.sq, data = daisy3)
(lm.lwpc.sum <- summary(lm.lwpc))
Call:
lm(formula = log(wpc) ~ vag_disch + milk120 + milk120.sq, data = daisy3)
Residuals:
Interval from wait period to conception
Min 1Q Median 3Q Max
-3.9229 -0.5554 0.0231 0.5794 1.7245
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.765e+00 3.140e-01 15.175 <2e-16 ***
vag_dischYes 1.477e-01 8.761e-02 1.686 0.0921 .
milk120 -4.664e-04 1.951e-04 -2.390 0.0170 *
milk120.sq 6.399e-08 2.965e-08 2.159 0.0310 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.7615 on 1521 degrees of freedom
Multiple R-squared: 0.006997, Adjusted R-squared: 0.005039
F-statistic: 3.573 on 3 and 1521 DF, p-value: 0.01356
(ci.lwpc <- confint(lm.lwpc)) # confidence intervals
2.5 % 97.5 %
(Intercept) 4.149060e+00 5.380862e+00
vag_dischYes -2.416148e-02 3.195190e-01
milk120 -8.491117e-04 -8.367357e-05
milk120.sq 5.844004e-09 1.221453e-07
exp(lm.lwpc$coefficients[2])
vag_dischYes
1.15914
exp(ci.lwpc[2, 1])
[1] 0.9761281
exp(ci.lwpc[2, 2])
[1] 1.376465
The trick to get the confidence interval is to get it on the transformed scale and then going back to the original scale. The most difficult part is in interpreting the results. A proprty of the logarithm is that “the difference between logs is the log of the ratio”. So the mean waiting period length difference between cows with and without vaginal discharge is 0.15 on a log scale, or exp(0.15) = 1.15 times longer for cows with vaginal discharge. Better maybe, express as ratios: the ratio of waiting periods from cows with vaginal discharge or no discharge is 1.15 (95% CI: 0.98 to 1.38). Note that the back-transformation of the confidence interval is not symmetric anymore.
So for your model , or
, an increase of 1 for
multiply the predicted response (in the original scale) by
(the regression coefficients are interpreted in a multiplicative rather than additive manner). If
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.