recycling accept-reject rejections (#2)
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
Following yesterday’s post on Rao’s, Liu’s, and Dunson’s paper on a new approach to intractable normalising constants, and taking advantage of being in Warwick, I tested the method on a toy model, namely the posterior associated with n Student’s t observations with unknown location parameter μ and a flat prior,
which is “naturally” bounded by a Cauchy density with scale √ν. The constant M is then easily derived and running the new algorithm follows from a normal random walk proposal targeting the augmented likelihood (R code below).
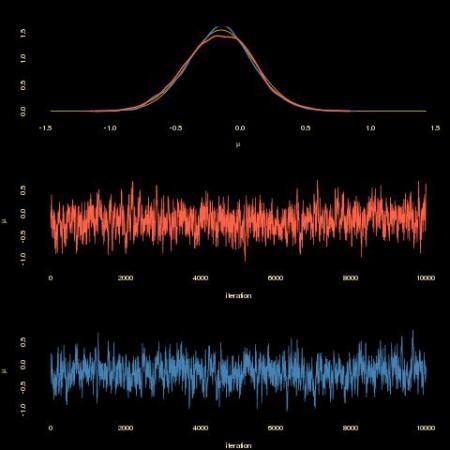 As shown by the above graph, the completion-by-rejection scheme produces a similar outcome (tomato) as the one based on the sole observations (steelblue). With a similar acceptance rate. However, the computing time is much much degraded:
As shown by the above graph, the completion-by-rejection scheme produces a similar outcome (tomato) as the one based on the sole observations (steelblue). With a similar acceptance rate. However, the computing time is much much degraded:
> system.time(g8()) user system elapsed 53.751 0.056 54.103 > system.time(g9()) user system elapsed 1.156 0.000 1.161
when compared with the no-completion version. Here is the entire R code that produced both MCMC samples:
#Student t observations and flat prior
nu=4
n=25
M=pi*sqrt(nu)
sqrtnu=sqrt(nu)
obs=rt(n,df=4)
sdobs=sd(obs)
#unormalised t
mydt=function(x,mu){
return(dt(x-mu,df=nu)/dt(0,df=nu))}
mydtc=cmpfun(mydt)
mydcauchy=function(x,mu){
y=(x-mu)/sqrtnu
return(dcauchy(y)/sqrtnu)}
mydcaucchy=cmpfun(mydcauchy)
#augmented data
augmen=function(mu){
y=NULL
for (i in 1:n){
prop=mu+rcauchy(1)*sqrtnu
reject=(runif(1)<mydtc(prop,mu)/(M*mydcaucchy(prop,mu)))
while (!reject){
y=c(y,prop)
prop=mu+rcauchy(1)*sqrtnu
reject=(runif(1)<mydtc(prop,mu)/(M*mydcaucchy(prop,mu)))}
}
return(y)}
#Gibbs
gibbsda=function(T=10^4){
theta=rep(0,T)
for (t in 2:T){
rej=augmen(theta[t-1])
theta[t]=prop=theta[t-1]+rnorm(1,sd=.1*sdobs)
propdens=sum(dt(obs-prop,df=nu,log=TRUE))+
sum(log(mydcaucchy(rej,prop)-mydtc(rej,mu=prop)/M))
refdens=sum(dt(obs-theta[t-1],df=nu,log=TRUE))+
sum(log(mydcaucchy(rej,theta[t-1])-mydtc(rej,mu=theta[t-1])/M))
if (log(runif(1))>propdens-refdens) theta[t]=theta[t-1]
}
return(theta)}
g8=cmpfun(gibbsda)
gibbs2=function(T=10^4){
eta=rep(0,T)
for (t in 2:T){
eta[t]=prop=eta[t-1]+rnorm(1,sd=sdobs)
propdens=sum(dt(obs-prop,df=nu,log=TRUE))
refdens=sum(dt(obs-eta[t-1],df=nu,log=TRUE))
if (log(runif(1))>propdens-refdens) eta[t]=eta[t-1]
}
return(eta)}
g9=cmpfun(gibbsda)
Filed under: R, Statistics, University life Tagged: accept-reject algorithm, compiler, Data augmentation, Gibbs sampling, MCMC, Monte Carlo Statistical Methods, Student’s t distribution
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
